A gráf felosztása diszjunkt körökre

Bizonyítás

A megmaradt gráf (az eredetihez hasonlóan) minden fokszáma páros, így ezen is elvégezhetjük a fönt leírtakat (addig, míg minden fokszám 0 lesz, tehát az összes élt föl nem használtuk), így további köröket fogunk találni.

Mivel véges számú él van, így a körök száma is véges lesz, tehát véges számú lépésen belül fölbontottuk a gráfot diszjunkt körökre.

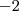
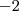Ha belépünk egy bizonyos csúcsba, akkor onnan biztosan ki is tudunk jönni, mivel ez összesen fokszám és kezdetben mindegyik fokszám páros. Így csak akkor tudunk elakadni, ha ahhoz a csúcshoz érünk, ahonnan a kört elkezdtük rajzolni. Mivel véges számú él van, ezért véges számú lépésen belül biztosan visszaérünk a kiválasztott csúcshoz, és el fogunk akadni, és létrejön egy kör (esetleg több is).