Az oldal tölt...
35
35
| Kategória: |
Bizonyítás
- Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Maradékosztályok |
Lektorálás: |
Nem lektorált |
A teljes maradékrendszer tétel
Bizonyítás
Bizonyítsuk be a tételt indirekt módon! Tegyük föl, hogy
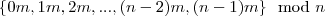
között van két egyenlő, legyenek ezek a maradékok
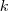
és
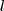
!
Ekkor
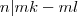
igaz, hiszen ez egyenértékű az
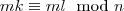
kifejezéssel.
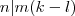
. Ezt és a kezdeti
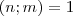
feltételt felhasználva nyilvánvalóan
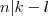
igaz.
Mivel a maradék kisebb, mint az osztó, így
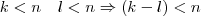
. Föntebb beláttuk, hogy

-nek oszthatónak kell lennie
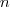
-nel, viszont

kisebb, mint
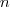
. Így
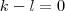
lehetséges csak, vagyis
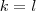
.
Tehát, ha valamely két tag egyenlő
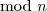
, akkor az a két tag saját maga. Így minden maradékból pontosan egy van, tehát beláttunk a tételt.
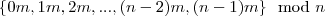 között van két egyenlő, legyenek ezek a maradékok
között van két egyenlő, legyenek ezek a maradékok 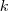 és
és 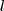 !
!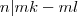 igaz, hiszen ez egyenértékű az
igaz, hiszen ez egyenértékű az 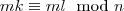 kifejezéssel.
kifejezéssel. 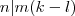 . Ezt és a kezdeti
. Ezt és a kezdeti 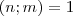 feltételt felhasználva nyilvánvalóan
feltételt felhasználva nyilvánvalóan 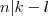 igaz.
igaz.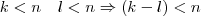 . Föntebb beláttuk, hogy
. Föntebb beláttuk, hogy  -nek oszthatónak kell lennie
-nek oszthatónak kell lennie 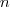 -nel, viszont
-nel, viszont  kisebb, mint
kisebb, mint 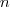 . Így
. Így 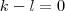 lehetséges csak, vagyis
lehetséges csak, vagyis 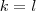 .
.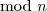 , akkor az a két tag saját maga. Így minden maradékból pontosan egy van, tehát beláttunk a tételt.
, akkor az a két tag saját maga. Így minden maradékból pontosan egy van, tehát beláttunk a tételt.




