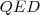Az oldal tölt...
166
166
| Kategória: |
Bizonyítás
- Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Ceva-egyenesek |
Lektorálás: |
Nem lektorált |
A Ceva-tétel és megfordítása
A Ceva-tétel bizonyítása
Ezeket a törteket a fönti egyenletbe behelyettesítve:
Észrevehető, hogy
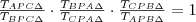
, mivel a tört egyszerűsíthető az
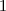
alakra.
Ahhoz, hogy a tétel teljesüljön, könnyen belátható, hogy az
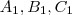
pontok közül vagy mindhárom rajta van a háromszög bizonyos oldalán (ekkor lehet közös metszéspont), vagy egy van rajta, a másik kettő csak az oldalegyenesén, nem az oldalán (ekkor a közös metszésponton kívül lehetnek párhuzamosak is az egyenesek). (Csak ebben a két esetben lehet egy közös metszéspont vagy párhuzamosság, a másik két esetben (amikor két pont van az oldalon, egy pedig az oldalegyenesen; vagy mindhárom pont csak az oldalegyenesen van rajta) mindig három különböző metszéspont létezik.) Így három esetet kell bizonyítanunk (és ennek megfordításait).
1. Mindhárom pont az oldalakon, közös metszéspont
2.a Két pont az oldalegyeneseken, egy az oldalon, közös metszéspont
A fenti megoldás mintájára bizonyítsuk be ezt az esetet!
Észrevehető, hogy
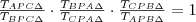
, mivel a tört egyszerűsíthető az
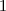
alakra.
Az így kapott egyenleteket helyettesítsük be a fönti egyenletbe!
2.b Két pont az oldalegyeneseken, egy az oldalon, párhuzamos egyenesek
Húzzunk be egy tetszőleges

egyenest, ami elmetszi a párhuzamos egyeneseket!
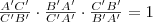
(Az egyszerűsítés után.)
A párhuzamos szelők tétele következtében az alábbi egyenleteket írhatjuk föl:
Ezeket a törteket a fönti egyenletbe behelyettesítve:
A Ceva-tétel megfordításának bizonyítása
3. Közös metszéspont
Legyen
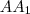
és
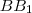
egyenesek metszéspontja
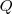
, a
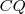
egyenes pedig messe az
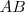
egyenest a
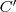
pontban! A Ceva-tétel szerint fölírhatjuk az alábbi összefüggést:
A tétel megfordítása állításának értelmében:
A két fölírt egyenletből:
Így a
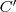
pont megegyezik a
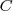
ponttal.
4. Párhuzamos egyenesek
Fönt leírtuk, hogyha
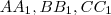
egyenesek közül bármely kettő metszi egymást (és
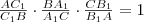
), akkor a harmadik is ezen a ponton megy át. Tehát, ha van metszéspont, akkor mindhárom egyenes ezen megy át. A továbbiakban azt az esetet vizsgáljuk, amikor
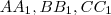
egyenesek közül két tetszőleges egyenesnek nincs metszéspontja, tehát párhuzamosak.
Legyen
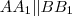
! Az ezekkel párhuzamos,
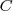
ponton átmenő egyenes messe
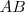
egyenesét
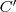
pontban! A Ceva-tétel szerint fölírhatjuk az alábbi összefüggést:
A tétel megfordítása állításának értelmében:
A két fölírt egyenletből:
Így a
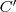
pont megegyezik a
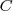
ponttal.
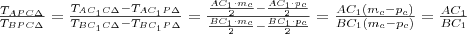 Hasonlóan:
Hasonlóan: 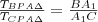 és
és 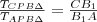 .
. 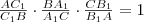
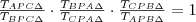 , mivel a tört egyszerűsíthető az
, mivel a tört egyszerűsíthető az 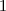 alakra.
alakra.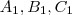 pontok közül vagy mindhárom rajta van a háromszög bizonyos oldalán (ekkor lehet közös metszéspont), vagy egy van rajta, a másik kettő csak az oldalegyenesén, nem az oldalán (ekkor a közös metszésponton kívül lehetnek párhuzamosak is az egyenesek). (Csak ebben a két esetben lehet egy közös metszéspont vagy párhuzamosság, a másik két esetben (amikor két pont van az oldalon, egy pedig az oldalegyenesen; vagy mindhárom pont csak az oldalegyenesen van rajta) mindig három különböző metszéspont létezik.) Így három esetet kell bizonyítanunk (és ennek megfordításait).
pontok közül vagy mindhárom rajta van a háromszög bizonyos oldalán (ekkor lehet közös metszéspont), vagy egy van rajta, a másik kettő csak az oldalegyenesén, nem az oldalán (ekkor a közös metszésponton kívül lehetnek párhuzamosak is az egyenesek). (Csak ebben a két esetben lehet egy közös metszéspont vagy párhuzamosság, a másik két esetben (amikor két pont van az oldalon, egy pedig az oldalegyenesen; vagy mindhárom pont csak az oldalegyenesen van rajta) mindig három különböző metszéspont létezik.) Így három esetet kell bizonyítanunk (és ennek megfordításait).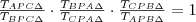 , mivel a tört egyszerűsíthető az
, mivel a tört egyszerűsíthető az 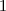 alakra.
alakra. 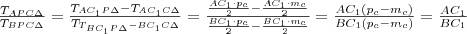 Hasonlóan:
Hasonlóan: 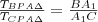 és
és 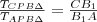 .
. 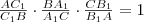
 egyenest, ami elmetszi a párhuzamos egyeneseket!
egyenest, ami elmetszi a párhuzamos egyeneseket!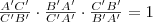 (Az egyszerűsítés után.)
(Az egyszerűsítés után.)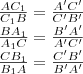
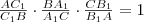
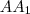 és
és 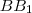 egyenesek metszéspontja
egyenesek metszéspontja 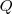 , a
, a 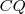 egyenes pedig messe az
egyenes pedig messe az 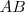 egyenest a
egyenest a 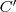 pontban! A Ceva-tétel szerint fölírhatjuk az alábbi összefüggést:
pontban! A Ceva-tétel szerint fölírhatjuk az alábbi összefüggést: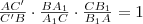
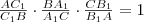
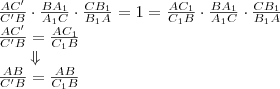
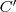 pont megegyezik a
pont megegyezik a 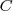 ponttal.
ponttal.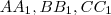 egyenesek közül bármely kettő metszi egymást (és
egyenesek közül bármely kettő metszi egymást (és 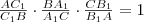 ), akkor a harmadik is ezen a ponton megy át. Tehát, ha van metszéspont, akkor mindhárom egyenes ezen megy át. A továbbiakban azt az esetet vizsgáljuk, amikor
), akkor a harmadik is ezen a ponton megy át. Tehát, ha van metszéspont, akkor mindhárom egyenes ezen megy át. A továbbiakban azt az esetet vizsgáljuk, amikor 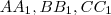 egyenesek közül két tetszőleges egyenesnek nincs metszéspontja, tehát párhuzamosak.
egyenesek közül két tetszőleges egyenesnek nincs metszéspontja, tehát párhuzamosak.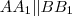 ! Az ezekkel párhuzamos,
! Az ezekkel párhuzamos, 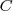 ponton átmenő egyenes messe
ponton átmenő egyenes messe 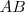 egyenesét
egyenesét 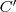 pontban! A Ceva-tétel szerint fölírhatjuk az alábbi összefüggést:
pontban! A Ceva-tétel szerint fölírhatjuk az alábbi összefüggést: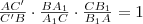
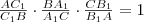
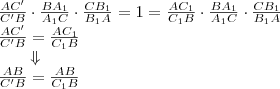
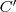 pont megegyezik a
pont megegyezik a 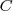 ponttal.
ponttal.