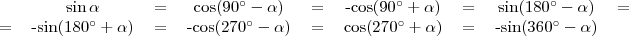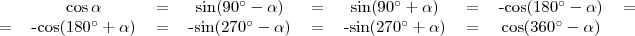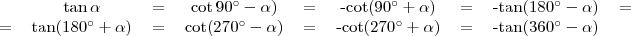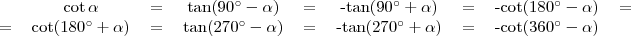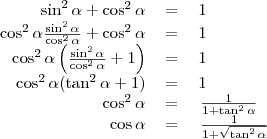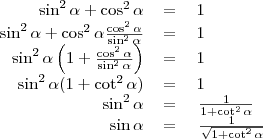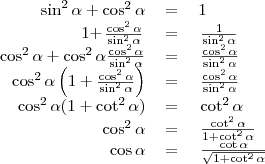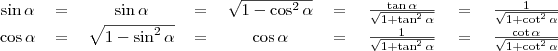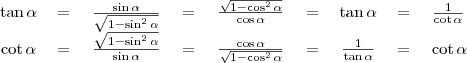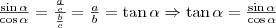Az oldal tölt...
158
158
| Kategória: |
Bizonyítás
- Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Trigonometrikus azonosságok (lásd még:04.BD és 04.CD) |
Lektorálás: |
Nem lektorált |
Az alapvető trigonometriai azonosságok
A Pitagorasz-tétel alapján:
1.b
2.
5.
Az egységsugarú körön húzzunk be

,
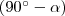
,
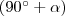
,
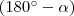
,
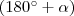
,
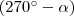
,
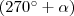
és
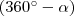
irányszögű, origó középpontú vektorokat (az ábrán feketével jelölve)! A vektorok tükörképei (kék) és a szögek szinuszai (zöld és piros) és koszinuszai (zöld és piros) egy-egy derékszögű háromszöget alkotnak. Ezek a háromszögek nyilvánvalóan egybevágóak (az azonos színű szakaszok egyenlő hosszúak). Az egyenlő hosszú szakaszokat kifejezem szögfüggvényekkel és egyenlővé teszem.
Bizonyítás
1.a
3.a
3.b
3.c
3.d
4.
5.a
5.b
5.c
5.d
Összegezve
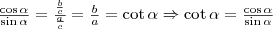
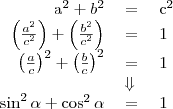
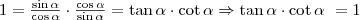
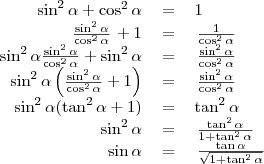
 ,
, 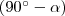 ,
, 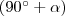 ,
, 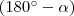 ,
, 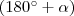 ,
, 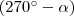 ,
, 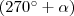 és
és 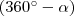 irányszögű, origó középpontú vektorokat (az ábrán feketével jelölve)! A vektorok tükörképei (kék) és a szögek szinuszai (zöld és piros) és koszinuszai (zöld és piros) egy-egy derékszögű háromszöget alkotnak. Ezek a háromszögek nyilvánvalóan egybevágóak (az azonos színű szakaszok egyenlő hosszúak). Az egyenlő hosszú szakaszokat kifejezem szögfüggvényekkel és egyenlővé teszem.
irányszögű, origó középpontú vektorokat (az ábrán feketével jelölve)! A vektorok tükörképei (kék) és a szögek szinuszai (zöld és piros) és koszinuszai (zöld és piros) egy-egy derékszögű háromszöget alkotnak. Ezek a háromszögek nyilvánvalóan egybevágóak (az azonos színű szakaszok egyenlő hosszúak). Az egyenlő hosszú szakaszokat kifejezem szögfüggvényekkel és egyenlővé teszem.