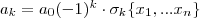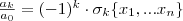Keresés
Legújabb cikkek
- Daniell-elem - definíció
- Akkumulátor - definíció
- Szárazelem - definíció
- Galvánelem - definíció
- Kirchhoff II. törvénye (huroktörvény) - törvény
Támogató
Szabványok
| Kategória: | Bizonyítás - Tétel | Évfolyam: | 9. |
| Kulcsszó: | Polinomok szorzattá alakítása | Lektorálás: | Nem lektorált |
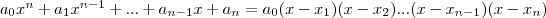
![\left[ a_0(-1)^0 \right]x^n+\left[a_0(-1)^1(x_1+x_2+x_3+...+x_{n-1}x_n)\right]x^{n-1}+\left[a_0(-1)^2\cdot \sigma_2\{x_1,...x_n\}\big]x^{n-2}+...+\big[a_0(-1)^{n-2}\cdot \sigma_{n-2}\{x_1,...x_n\} \big]x^2+\big[a_0(-1)^{n-1}\cdot \sigma_{n-1}\{x_1,...x_n\}\big]x+\big[a_0(-1)^n(x_1x_2x_3\cdot ...\cdot x_{n-1}x_n)\big]](libraries/modulok/latexesszoveg/media/latex/6a3362c19572c0aeca08e3498bfe7680.png "\left[ a_0(-1)^0 \right]x^n+\left[a_0(-1)^1(x_1+x_2+x_3+...+x_{n-1}x_n)\right]x^{n-1}+\left[a_0(-1)^2\cdot \sigma_2\{x_1,...x_n\}\big]x^{n-2}+...+\big[a_0(-1)^{n-2}\cdot \sigma_{n-2}\{x_1,...x_n\} \big]x^2+\big[a_0(-1)^{n-1}\cdot \sigma_{n-1}\{x_1,...x_n\}\big]x+\big[a_0(-1)^n(x_1x_2x_3\cdot ...\cdot x_{n-1}x_n)\big]")
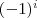az előjelét határozza meg. A most kapott, és az eredeti polinom azonos fokú együtthatóinak meg kell egyeznie, hiszen a két polinom egyenlő. Észrevéve az általános formulát a két azonos fokú együttható a következőt írhatjuk föl:
