Az oldal tölt...
99
99
| Kategória: |
Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Másodfokú függvények |
Lektorálás: |
Nem lektorált |
A másodfokú függvény
"A másodfokú egyenlet általános megoldása" című bizonyításnál leírtakhoz hasonlóan a fönti alak átalakítható a következőre:
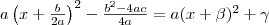
.
Tulajdonságok
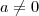
, mert ekkor lineáris függvényt kapunk.
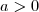
Ebben az esetben az ábrázolt parabola felfelé nyílik, minimuma létezik
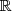
-en.
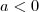
Ebben az esetben a parabola lefelé nyílik, maximuma létezik
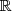
-en.
Az
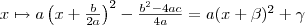
alakból jól látható, hogy a
szélsőérték helye:
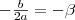
, míg a
szélsőérték:
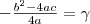
.
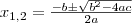
a másodfokú függvény zérushelyei.
Tengelyes affinitás (

tengely irányában)

-val.
Eltolás

tengely mentén
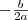
.
Eltolás
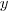
tengely mentén
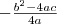
.
Monotonitás
A
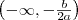
és
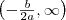
intervallumon is szigorúan monoton.
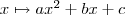
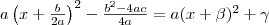 .
.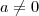 , mert ekkor lineáris függvényt kapunk.
, mert ekkor lineáris függvényt kapunk.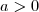 Ebben az esetben az ábrázolt parabola felfelé nyílik, minimuma létezik
Ebben az esetben az ábrázolt parabola felfelé nyílik, minimuma létezik 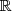 -en.
-en.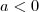 Ebben az esetben a parabola lefelé nyílik, maximuma létezik
Ebben az esetben a parabola lefelé nyílik, maximuma létezik 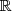 -en.
-en. 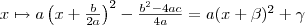 alakból jól látható, hogy a
alakból jól látható, hogy a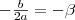 , míg a
, míg a 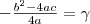 .
.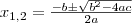 a másodfokú függvény zérushelyei.
a másodfokú függvény zérushelyei. tengely irányában)
tengely irányában)  -val.
-val. tengely mentén
tengely mentén 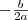 .
.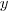 tengely mentén
tengely mentén 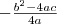 .
.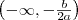 és
és 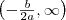 intervallumon is szigorúan monoton.
intervallumon is szigorúan monoton.




