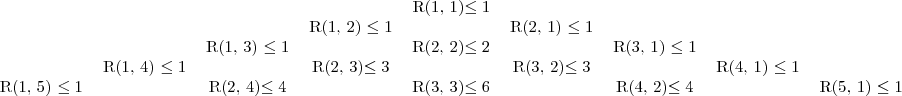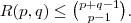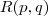Az oldal tölt...
82
82
| Kategória: |
Bizonyítás
- Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Ramsey-gráfok |
Lektorálás: |
Nem lektorált |
A kétargumentumú Ramsey-számok felső becslése
Bizonyítás
Egy teljes gráfban színezzük be az éleket pirossal és kékkel! Ha egy csúcsból kiindul adott számú kékszínű él, akkor a "végpontok" által meghatározott gráfban biztosan lennie kell egy

csúcsú teljes részgráfnak (a "kezdő" csúcs lesz a
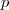
-edik), vagy egy
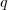
csúcsú teljes részgráfnak (a saját színéből). Így ahhoz, hogy még adható legyen ellenpélda (hogy ne legyen biztosan vagy kék színű
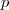
csúcsú teljes részgráf, vagy piros színű
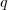
csúcsú teljes részgráf)a kék színű csúcsok száma
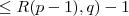
. Hasonlóan a piros fokok száma
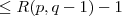
.
Tehát hogy adható lehessen ellenpélda csúcsonkénti fokszám legfeljebb
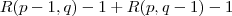
lehet; azaz a csúcsok száma legfeljebb
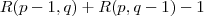
. Ahhoz, hogy nem lehessen már ellenpélda, kell még egy él (még egy csúcs), így biztosan létrejön vagy kék színű
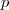
csúcsú teljes részgráf, vagy piros színű
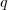
csúcsú teljes részgráf. Így a
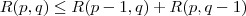
rekurzív formula állapítható meg.
Vizsgáljuk meg az első néhány Ramsey-szám értékét!
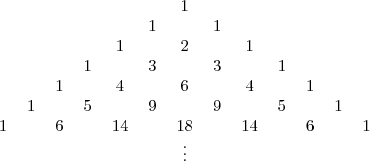
Mivel az első néhány elem és a rekurzív formula is megegyezik a Pascal-háromszögével, így
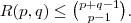
Ez csak felsőbecslés. A valódi táblázat a következő (az égész táblázat nem ismert):
 csúcsú teljes részgráfnak (a "kezdő" csúcs lesz a
csúcsú teljes részgráfnak (a "kezdő" csúcs lesz a 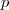 -edik), vagy egy
-edik), vagy egy 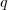 csúcsú teljes részgráfnak (a saját színéből). Így ahhoz, hogy még adható legyen ellenpélda (hogy ne legyen biztosan vagy kék színű
csúcsú teljes részgráfnak (a saját színéből). Így ahhoz, hogy még adható legyen ellenpélda (hogy ne legyen biztosan vagy kék színű 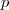 csúcsú teljes részgráf, vagy piros színű
csúcsú teljes részgráf, vagy piros színű 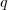 csúcsú teljes részgráf)a kék színű csúcsok száma
csúcsú teljes részgráf)a kék színű csúcsok száma 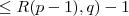 . Hasonlóan a piros fokok száma
. Hasonlóan a piros fokok száma 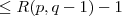 .
.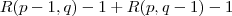 lehet; azaz a csúcsok száma legfeljebb
lehet; azaz a csúcsok száma legfeljebb 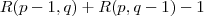 . Ahhoz, hogy nem lehessen már ellenpélda, kell még egy él (még egy csúcs), így biztosan létrejön vagy kék színű
. Ahhoz, hogy nem lehessen már ellenpélda, kell még egy él (még egy csúcs), így biztosan létrejön vagy kék színű 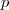 csúcsú teljes részgráf, vagy piros színű
csúcsú teljes részgráf, vagy piros színű 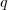 csúcsú teljes részgráf. Így a
csúcsú teljes részgráf. Így a 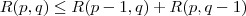 rekurzív formula állapítható meg.
rekurzív formula állapítható meg.