Az oldal tölt...
67
67
| Kategória: |
Bizonyítás
- Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Egyszerű gráfok |
Lektorálás: |
Nem lektorált |
Az azonos fokszámú csúcsok tétele
Tegyük föl, hogy minden csúcs fokszáma különböző! Ekkor az
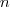
csúcsú gráfban a fokszámok biztosan
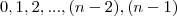
. A
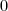
fokszámú semelyik csúccsal sincs összekötve, míg az

fokszámú csúcsnak minden másik csúccsal össze van kötve. Ez ellentmondás, tehát hamis feltételből indultunk ki, így a tételt igazoltuk.
A tétel végtelen (végtelen csúcsból álló gráf) egyszerű gráfra nyilvánvalóan nem igaz, erre könnyen adható ellenpélda:
Bizonyítás
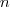 csúcsú gráfban a fokszámok biztosan
csúcsú gráfban a fokszámok biztosan 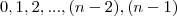 . A
. A 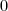 fokszámú semelyik csúccsal sincs összekötve, míg az
fokszámú semelyik csúccsal sincs összekötve, míg az  fokszámú csúcsnak minden másik csúccsal össze van kötve. Ez ellentmondás, tehát hamis feltételből indultunk ki, így a tételt igazoltuk.
fokszámú csúcsnak minden másik csúccsal össze van kötve. Ez ellentmondás, tehát hamis feltételből indultunk ki, így a tételt igazoltuk.




