Az oldal tölt...
37
37
| Kategória: |
Bizonyítás
|
Évfolyam: |
9. |
| Kulcsszó: |
Lineáris kongruenciák |
Lektorálás: |
Nem lektorált |
A lineáris kongruencia
Általános levezetés
A bal oldal osztható
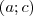
-val, mert
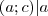
. A jobb oldalon

is osztható
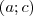
-val. Így akkor és csak akkor lehet megoldása a kongruenciának, hogyha
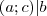
(később belátjuk, hogy ilyenkor mindig van megoldás). Ha ez fennáll, akkor
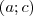
-val leosztjuk a kongruenciát.
Ekkor nyilvánvalóan
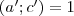
, tehát pontosan egy megoldás létezik
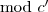
, mivel ez egy teljes maradékrendszer. Így
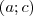
darab megoldás van
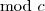
. Az
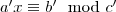
alak egyenértékű az
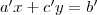
alakkal.
Innentől a levezetés részletesen megtalálható "Az elsőfokú diofantoszi egyenlet" című bizonyításnál, így a következőkben csak nagyvonalakban vázolom föl a bizonyítás további részét.
Az euklideszi algoritmus segítségével megkeressük az
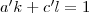
egyenlet
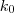
és
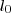
megoldását. Ebből

és
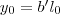
. Ezek az
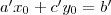
egyenlet megoldásai. Ezt kongruenciaalakba átírva:
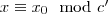
.
Az eredeti kongruenciára így a (legnagyobb közös osztóval történő beszorzás után)
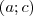
számú megoldás van:
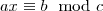
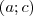 -val, mert
-val, mert 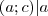 . A jobb oldalon
. A jobb oldalon  is osztható
is osztható 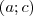 -val. Így akkor és csak akkor lehet megoldása a kongruenciának, hogyha
-val. Így akkor és csak akkor lehet megoldása a kongruenciának, hogyha 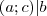 (később belátjuk, hogy ilyenkor mindig van megoldás). Ha ez fennáll, akkor
(később belátjuk, hogy ilyenkor mindig van megoldás). Ha ez fennáll, akkor 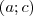 -val leosztjuk a kongruenciát.
-val leosztjuk a kongruenciát.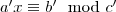
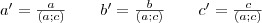
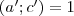 , tehát pontosan egy megoldás létezik
, tehát pontosan egy megoldás létezik 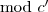 , mivel ez egy teljes maradékrendszer. Így
, mivel ez egy teljes maradékrendszer. Így 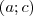 darab megoldás van
darab megoldás van 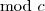 . Az
. Az 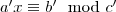 alak egyenértékű az
alak egyenértékű az 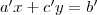 alakkal.
alakkal. 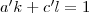 egyenlet
egyenlet 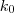 és
és 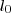 megoldását. Ebből
megoldását. Ebből  és
és 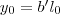 . Ezek az
. Ezek az 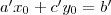 egyenlet megoldásai. Ezt kongruenciaalakba átírva:
egyenlet megoldásai. Ezt kongruenciaalakba átírva: 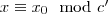 .
.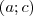 számú megoldás van:
számú megoldás van:![x \equiv \begin{cases}
x_0 \\
x_0+c' \\
x_0+2c' \\
\vdots & \mod c\\
x_0+\big[ (a; c)-3 \big]c' \\
x_0+\big[ (a; c)-2 \big]c' \\
x_0+\big[ (a; c)-1 \big]c'
\end{cases} x \equiv \begin{cases}
x_0 \\
x_0+c' \\
x_0+2c' \\
\vdots & \mod c\\
x_0+\big[ (a; c)-3 \big]c' \\
x_0+\big[ (a; c)-2 \big]c' \\
x_0+\big[ (a; c)-1 \big]c'
\end{cases}](libraries/modulok/latexesszoveg/media/latex/1905e17962d52d5ec4ca476eefa6991c.png)





