Az oldal tölt...
32
32
| Kategória: |
Bizonyítás
|
Évfolyam: |
9. |
| Kulcsszó: |
Elsőfokú diofantikus egyenletek, egyenlőtlenségek |
Lektorálás: |
Nem lektorált |
Az elsőfokú diofantoszi egyenlet
Elsőfokú diofantoszi egyenlet általános megoldása
Az általános elsőfokú diofantoszi egyenletet a következő módon szokás fölírni:
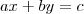
(

,

és

paraméter).
A bal oldala nyilvánvalóan osztható
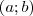
-val, így ahhoz, hogy az egyenlet megoldható legyen teljesülnie kell a következő feltételnek:
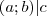
(Később belátjuk, hogy ha ez a feltétel teljesül, akkor mindig megoldható az egyenlet az egész számok körében.) Ha ez teljesül, akkor leosztom
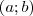
-val az egyenletet.
Az euklideszi algoritmus segítségével keresünk olyan
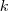
és
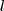
számokat, amelyekre
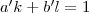
. (Ilyet biztosan találunk, mert
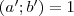
és az algoritmus ezen két számot vonja ki addig egymásból - a maradékos osztás lényegében véges sokszor elvégzett kivonás -, amíg megkapjuk a legnagyobb közös osztót, jelen esetben az
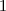
-t.)
Példa
Végezzük el erre a két számra az euklideszi algoritmus lépéseit!
Most a jobb oldali egyenletekből fejezzük ki az 1-et 51 és 23 felhasználásával!
Ebben az esetben
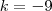
és
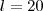
adódott.
Levezetés - folytatás
A már megoldott
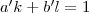
egyenletet szorozzuk be
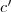
-vel! Így megkaptuk az
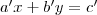
megoldását:

és
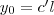
. Ezt
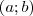
-val szorozva megkapjuk az eredeti,
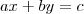
egyenletet és így a megoldásait. Észrevehető, hogy
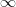
sok megoldás létezik. Ezeket a következő módon képezzük:
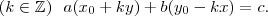
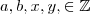
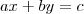 (
( ,
,  és
és  paraméter).
paraméter).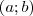 -val, így ahhoz, hogy az egyenlet megoldható legyen teljesülnie kell a következő feltételnek:
-val, így ahhoz, hogy az egyenlet megoldható legyen teljesülnie kell a következő feltételnek: 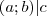 (Később belátjuk, hogy ha ez a feltétel teljesül, akkor mindig megoldható az egyenlet az egész számok körében.) Ha ez teljesül, akkor leosztom
(Később belátjuk, hogy ha ez a feltétel teljesül, akkor mindig megoldható az egyenlet az egész számok körében.) Ha ez teljesül, akkor leosztom 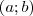 -val az egyenletet.
-val az egyenletet.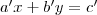
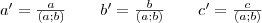
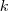 és
és 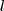 számokat, amelyekre
számokat, amelyekre 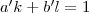 . (Ilyet biztosan találunk, mert
. (Ilyet biztosan találunk, mert 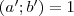 és az algoritmus ezen két számot vonja ki addig egymásból - a maradékos osztás lényegében véges sokszor elvégzett kivonás -, amíg megkapjuk a legnagyobb közös osztót, jelen esetben az
és az algoritmus ezen két számot vonja ki addig egymásból - a maradékos osztás lényegében véges sokszor elvégzett kivonás -, amíg megkapjuk a legnagyobb közös osztót, jelen esetben az 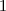 -t.)
-t.)
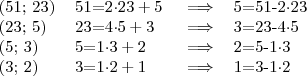
![1=3-1\cdot 2=3-1\cdot (5-1\cdot 3)=23-4\cdot 5-1\cdot (5-1\cdot (23-4\cdot 5)=23-4\cdot (51-2\cdot 23)-1\cdot \bigg[(51-2\cdot 23)-1\cdot \Big(23-4\cdot (51-2\cdot 23)\Big)\bigg]=20\cdot 23-9\cdot 51=1 1=3-1\cdot 2=3-1\cdot (5-1\cdot 3)=23-4\cdot 5-1\cdot (5-1\cdot (23-4\cdot 5)=23-4\cdot (51-2\cdot 23)-1\cdot \bigg[(51-2\cdot 23)-1\cdot \Big(23-4\cdot (51-2\cdot 23)\Big)\bigg]=20\cdot 23-9\cdot 51=1](libraries/modulok/latexesszoveg/media/latex/7d91ef07248e0621a6159c2a55847606.png)
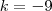 és
és 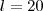 adódott.
adódott.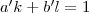 egyenletet szorozzuk be
egyenletet szorozzuk be 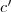 -vel! Így megkaptuk az
-vel! Így megkaptuk az 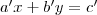 megoldását:
megoldását:  és
és 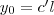 . Ezt
. Ezt 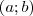 -val szorozva megkapjuk az eredeti,
-val szorozva megkapjuk az eredeti, 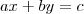 egyenletet és így a megoldásait. Észrevehető, hogy
egyenletet és így a megoldásait. Észrevehető, hogy 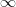 sok megoldás létezik. Ezeket a következő módon képezzük:
sok megoldás létezik. Ezeket a következő módon képezzük: