Az oldal tölt...
303
303
| Kategória: |
Bizonyítás
|
Évfolyam: |
10. |
| Kulcsszó: |
Ideális gáz nyomásának értelmezése (alapegyenlet) |
Lektorálás: |
Nem lektorált |
Ideális gáz nyomásának mikroszkopikus értelmezése
Az alábbiakban az ideális gáz nyomását értelmezzük egy

-
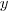
-

élhosszúságú téglatest alakú tartályban. Ideális gázban a részecskék egymással való kölcsönhatásaitól eltekinthetünk, a részecskék tehát csak az edény falával ütközhetnek.
Tekintsünk egy részecskét! Ha ez a részecske az edény
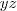
oldalakkal határolt falával ütközik,

irányú sebessége ellentettjére változik, tehát az edénynek átadott impulzusa
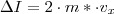
, ahol
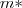
a részecske tömege,
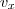
az

irányú sebessége. Két, ugyanezzel a lappal való ütközés közt eltelt idő
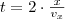
. Tehát
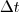
idő alatt lezajló ütközések száma
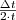
. Adott idő alatt az edény eme lapjának átadott impulzusmennyiség:
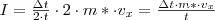
.
Az edény
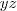
lapjára e részecske által kifejtett erő átlagos nagysága:
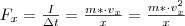
. Az edény
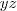
lapjára a gáz által kifejtett átlagos erőnagyság:
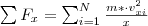
A részecskék

irányú sebességük négyzetének átlaga
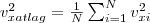
. Ezt behelyettesítve az átlagos erőnagyságra vonatkozó képletünkbe:
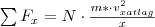
. Mivel ideális gázt vizsgálunk, ezért tekinthetjük a részecskék

,
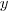
és

irányú sebességét egyenlőnek. A térbeli Pithagorasz-tétel értelmében
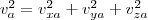
, ahol
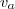
a részecskék átlagos sebessége,
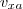
,
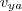
és

pedig a részecskék átlagos adott irányú sebessége.
Ezt behelyettesítve az előző képletünkbe:
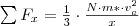
. A nyomás definíciója szerint
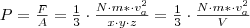
, ahol
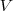
az edény térfogata.
 -
- 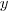 -
-  élhosszúságú téglatest alakú tartályban. Ideális gázban a részecskék egymással való kölcsönhatásaitól eltekinthetünk, a részecskék tehát csak az edény falával ütközhetnek.
élhosszúságú téglatest alakú tartályban. Ideális gázban a részecskék egymással való kölcsönhatásaitól eltekinthetünk, a részecskék tehát csak az edény falával ütközhetnek.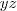 oldalakkal határolt falával ütközik,
oldalakkal határolt falával ütközik,  irányú sebessége ellentettjére változik, tehát az edénynek átadott impulzusa
irányú sebessége ellentettjére változik, tehát az edénynek átadott impulzusa 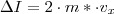 , ahol
, ahol 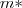 a részecske tömege,
a részecske tömege, 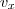 az
az  irányú sebessége. Két, ugyanezzel a lappal való ütközés közt eltelt idő
irányú sebessége. Két, ugyanezzel a lappal való ütközés közt eltelt idő 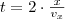 . Tehát
. Tehát 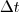 idő alatt lezajló ütközések száma
idő alatt lezajló ütközések száma 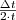 . Adott idő alatt az edény eme lapjának átadott impulzusmennyiség:
. Adott idő alatt az edény eme lapjának átadott impulzusmennyiség: 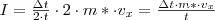 .
.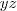 lapjára e részecske által kifejtett erő átlagos nagysága:
lapjára e részecske által kifejtett erő átlagos nagysága: 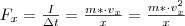 . Az edény
. Az edény 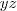 lapjára a gáz által kifejtett átlagos erőnagyság:
lapjára a gáz által kifejtett átlagos erőnagyság: 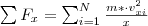
 irányú sebességük négyzetének átlaga
irányú sebességük négyzetének átlaga 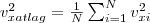 . Ezt behelyettesítve az átlagos erőnagyságra vonatkozó képletünkbe:
. Ezt behelyettesítve az átlagos erőnagyságra vonatkozó képletünkbe: 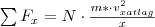 . Mivel ideális gázt vizsgálunk, ezért tekinthetjük a részecskék
. Mivel ideális gázt vizsgálunk, ezért tekinthetjük a részecskék  ,
, 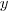 és
és  irányú sebességét egyenlőnek. A térbeli Pithagorasz-tétel értelmében
irányú sebességét egyenlőnek. A térbeli Pithagorasz-tétel értelmében 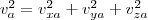 , ahol
, ahol 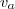 a részecskék átlagos sebessége,
a részecskék átlagos sebessége, 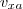 ,
, 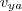 és
és  pedig a részecskék átlagos adott irányú sebessége.
pedig a részecskék átlagos adott irányú sebessége. 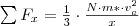 . A nyomás definíciója szerint
. A nyomás definíciója szerint 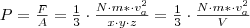 , ahol
, ahol 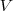 az edény térfogata.
az edény térfogata.




