Az oldal tölt...
29
29
| Kategória: |
Bizonyítás
- Definíció
|
Évfolyam: |
9. |
| Kulcsszó: |
Euklideszi algoritmus |
Lektorálás: |
Nem lektorált |
Az euklideszi algoritmus
Az euklideszi algoritmus helyességének levezetése
Az

számhoz található olyan
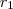
és
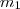
(nevezetesen az

-nak a

-vel való maradékos osztásának eredménye és maradéka), amelyekre a következő feltételek teljesülnek:
Ha két számnak van egy közös osztója, akkor ezzel a számmal a két szám különbsége is osztható lesz. Így
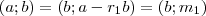
Hasonlóan a

számhoz is található olyan
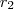
és
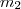
, amelyekre a következő feltételek teljesülnek:
Ezt a folyamatot addig folytatjuk, amíg
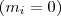
. (Mivel a maradékok minden lépés után csökkennek, ezért egy idő után lesz egy ilyen állapot.)
Így megkaptuk

és

számpár legnagyobb közös osztóját.
Következmény
Van olyan
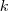
és
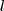
egész szám, hogy
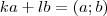

és

ugyanis felírható ilyen alakban, és így sorra minden
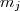
is, mert az
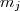
-t két ilyen alakban felírható szám különbségeként kapjuk.
Példa
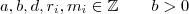
 számhoz található olyan
számhoz található olyan 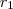 és
és 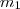 (nevezetesen az
(nevezetesen az  -nak a
-nak a  -vel való maradékos osztásának eredménye és maradéka), amelyekre a következő feltételek teljesülnek:
-vel való maradékos osztásának eredménye és maradéka), amelyekre a következő feltételek teljesülnek: 
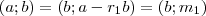
 számhoz is található olyan
számhoz is található olyan 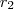 és
és 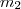 , amelyekre a következő feltételek teljesülnek:
, amelyekre a következő feltételek teljesülnek: 
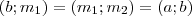
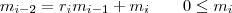
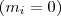 . (Mivel a maradékok minden lépés után csökkennek, ezért egy idő után lesz egy ilyen állapot.)
. (Mivel a maradékok minden lépés után csökkennek, ezért egy idő után lesz egy ilyen állapot.) 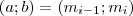 . De mivel
. De mivel 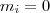 , így
, így 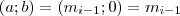
 és
és  számpár legnagyobb közös osztóját.
számpár legnagyobb közös osztóját. 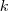 és
és 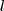 egész szám, hogy
egész szám, hogy 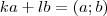
 és
és  ugyanis felírható ilyen alakban, és így sorra minden
ugyanis felírható ilyen alakban, és így sorra minden 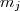 is, mert az
is, mert az 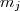 -t két ilyen alakban felírható szám különbségeként kapjuk.
-t két ilyen alakban felírható szám különbségeként kapjuk.