Az oldal tölt...
206
206
| Kategória: |
Bizonyítás
- Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Magasságpont |
Lektorálás: |
Nem lektorált |
A magasságpont oldalak felezőpontjára vett tükörképei
Bizonyítás
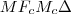
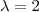
-szeres
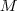
középpontú nagyított képe
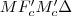
, így
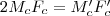
. Mivel
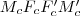
négyszög téglalap, így
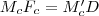
. Tehát az két fölírt egyenletből:
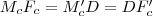
.
Ha a kört
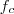
-re tükrözzük, önmagát kapjuk meg. Mivel
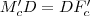
, így
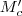
-t
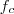
-re tükrözve
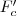
-re jutunk. De mivel "A magasságpont oldalakra vett tükörképei" című bizonyításnál beláttuk, hogy
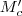
rajta van a körülírt körön, így
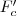
is rajta van a körülírt körön.
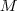
a magasságpont,
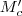
pont
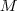
-nek
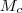
-re tükrözött képe,
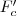
pont
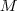
-nek
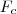
-re tükrözött képe és
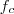
az
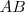
oldal felezőmerőlegese.
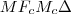
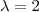 -szeres
-szeres 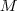 középpontú nagyított képe
középpontú nagyított képe 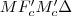 , így
, így 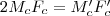 . Mivel
. Mivel 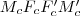 négyszög téglalap, így
négyszög téglalap, így 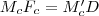 . Tehát az két fölírt egyenletből:
. Tehát az két fölírt egyenletből: 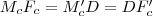 .
.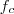 -re tükrözzük, önmagát kapjuk meg. Mivel
-re tükrözzük, önmagát kapjuk meg. Mivel 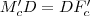 , így
, így 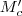 -t
-t 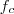 -re tükrözve
-re tükrözve 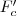 -re jutunk. De mivel "A magasságpont oldalakra vett tükörképei" című bizonyításnál beláttuk, hogy
-re jutunk. De mivel "A magasságpont oldalakra vett tükörképei" című bizonyításnál beláttuk, hogy 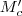 rajta van a körülírt körön, így
rajta van a körülírt körön, így 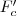 is rajta van a körülírt körön.
is rajta van a körülírt körön. 
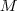 a magasságpont,
a magasságpont, 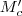 pont
pont 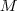 -nek
-nek 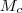 -re tükrözött képe,
-re tükrözött képe, 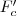 pont
pont 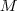 -nek
-nek 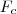 -re tükrözött képe és
-re tükrözött képe és 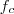 az
az 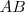 oldal felezőmerőlegese.
oldal felezőmerőlegese.




