Az oldal tölt...
200
200
| Kategória: |
Bizonyítás
- Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Magasságpont |
Lektorálás: |
Nem lektorált |
A magasságpont oldalakra vett tükörképei
Bizonyítás
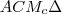
belső szögeinek összege megegezik
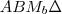
-ével.
"A középponti és kerületi szögek tétele" miatt
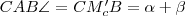
, mivel
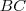
közös húr.
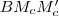
háromszögben:
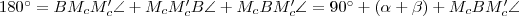
, tehát
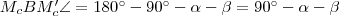
. De mivel
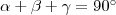
, így
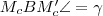
.
Hasonlóan
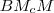
háromszögben:
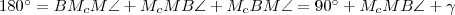
, tehát
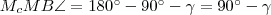
. De mivel
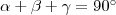
, így
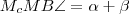
.
Tehát
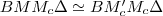
, mert mindhárom szögük páronként megegyezik, és van egy közös,
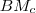
oldaluk.
Következésképp
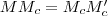
, tehát a magasságpontot az oldalra (vagy az magasságvonal talppontjára) tükrözve a körülírt körre jutunk. (A bizonyítás elvégezhető mindhárom oldalra.)
Az
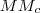
egyenes messe a körülírt kört
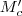
pontban!
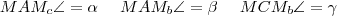
.
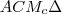 belső szögeinek összege megegezik
belső szögeinek összege megegezik 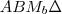 -ével.
-ével.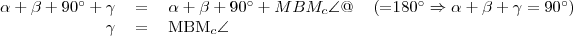
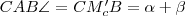 , mivel
, mivel 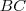 közös húr.
közös húr.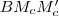 háromszögben:
háromszögben: 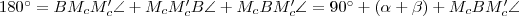 , tehát
, tehát 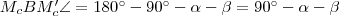 . De mivel
. De mivel 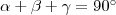 , így
, így 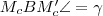 .
.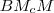 háromszögben:
háromszögben: 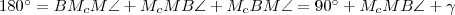 , tehát
, tehát 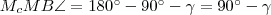 . De mivel
. De mivel 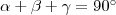 , így
, így 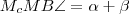 .
.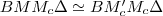 , mert mindhárom szögük páronként megegyezik, és van egy közös,
, mert mindhárom szögük páronként megegyezik, és van egy közös, 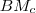 oldaluk.
oldaluk.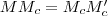 , tehát a magasságpontot az oldalra (vagy az magasságvonal talppontjára) tükrözve a körülírt körre jutunk. (A bizonyítás elvégezhető mindhárom oldalra.)
, tehát a magasságpontot az oldalra (vagy az magasságvonal talppontjára) tükrözve a körülírt körre jutunk. (A bizonyítás elvégezhető mindhárom oldalra.)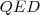
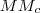 egyenes messe a körülírt kört
egyenes messe a körülírt kört 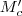 pontban!
pontban! 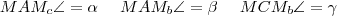 .
.




