Az oldal tölt...
193
193
| Kategória: |
Bizonyítás
- Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Apollonios-kör |
Lektorálás: |
Nem lektorált |
Az Apollóniusz-kör
Bizonyítás
Írjuk föl a Pitagorasz-tételt az
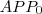
háromszögre!
Majd a
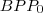
háromszögre!
A kapott egyenlet egy köregyenlet. Tehát az említett tulajdonságú pontok a
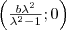
középpontú,
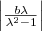
sugarú körön helyezkednek el.
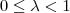
intervallumban a körök középpontjai az

tengelyen az
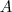
ponttól balra helyezkednek el. Minél messzebb van a középpontja ettől a ponttól, annál nagyobb a sugara.
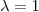
esetben
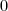
-val osztunk. Így ezt a törtet értelmezhetjük végtelenként is. Ekkor a kör középpontja a

vagy
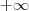
pontban van és a sugara
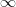
hosszú. Ez valójában az
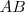
szakasz felezőmerőlegese.
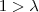
intervallumban pedig a körök középpontjai az

tengelyen az
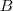
ponttól jobbra helyezkednek el. Minél messzebb van a középpontja ettől a ponttól, annál nagyobb a sugara.
Az arány legyen
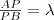
!
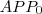 háromszögre!
háromszögre!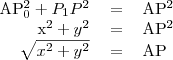
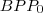 háromszögre!
háromszögre! 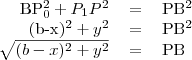
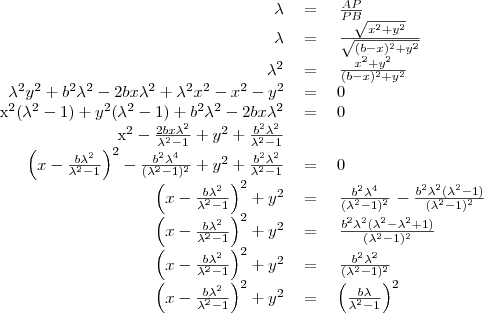
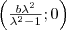 középpontú,
középpontú, 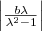 sugarú körön helyezkednek el.
sugarú körön helyezkednek el.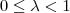 intervallumban a körök középpontjai az
intervallumban a körök középpontjai az  tengelyen az
tengelyen az 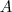 ponttól balra helyezkednek el. Minél messzebb van a középpontja ettől a ponttól, annál nagyobb a sugara.
ponttól balra helyezkednek el. Minél messzebb van a középpontja ettől a ponttól, annál nagyobb a sugara.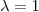 esetben
esetben 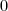 -val osztunk. Így ezt a törtet értelmezhetjük végtelenként is. Ekkor a kör középpontja a
-val osztunk. Így ezt a törtet értelmezhetjük végtelenként is. Ekkor a kör középpontja a  vagy
vagy 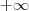 pontban van és a sugara
pontban van és a sugara 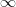 hosszú. Ez valójában az
hosszú. Ez valójában az 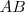 szakasz felezőmerőlegese.
szakasz felezőmerőlegese.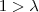 intervallumban pedig a körök középpontjai az
intervallumban pedig a körök középpontjai az  tengelyen az
tengelyen az 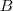 ponttól jobbra helyezkednek el. Minél messzebb van a középpontja ettől a ponttól, annál nagyobb a sugara.
ponttól jobbra helyezkednek el. Minél messzebb van a középpontja ettől a ponttól, annál nagyobb a sugara. 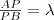 !
!




