Az oldal tölt...
191
191
| Kategória: |
Bizonyítás
- Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Trigonometria – szögfüggvények |
Lektorálás: |
Nem lektorált |
A szinusztétel
Tükrözzük
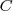
pontot az
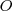
középpontra! Az így kapott
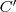
pontot kössük össze
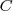
és
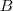
pontokkal!
"A középponti és kerületi szögek tétele" miatt
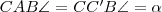
. "A Thalész-tétel" miatt pedig

. Írjuk föl a
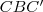
derékszögű háromszögben az

szög szinuszát!
Ezt minden oldalra elvégezhetjük, így megkapjuk a
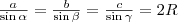
összefüggést.
I.
II.
Írjuk föl az

és a
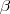
szög szinuszát!
A két egyenletet egymással elosztjuk:
Ezt minden oldalpárra elvégezhetjük, így
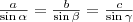
.
Tudjuk, hogy
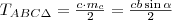
és
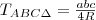
Így
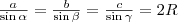
.
Bizonyítás
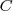 pontot az
pontot az 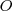 középpontra! Az így kapott
középpontra! Az így kapott 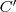 pontot kössük össze
pontot kössük össze 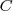 és
és 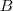 pontokkal!
pontokkal! 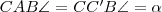 . "A Thalész-tétel" miatt pedig
. "A Thalész-tétel" miatt pedig  . Írjuk föl a
. Írjuk föl a 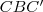 derékszögű háromszögben az
derékszögű háromszögben az  szög szinuszát!
szög szinuszát!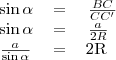
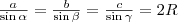 összefüggést.
összefüggést. és a
és a 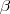 szög szinuszát!
szög szinuszát!
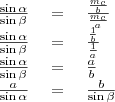
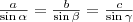 .
. 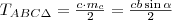 és
és 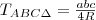
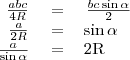
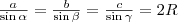 .
.