Az oldal tölt...
189
189
| Kategória: |
Megoldás
- Feladat
|
Évfolyam: |
9. |
| Kulcsszó: |
Kör |
Lektorálás: |
Nem lektorált |
Három kör "hatványvonala"
Megoldás
Húzzuk be mindegyik körpár hatványvonalát!
Tekintsük
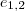
és
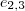
hatványvonalát! Nevezzük a metszéspontot
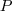
-nek. A
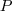
pont
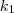
és
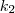
körökre vonatkozó hatványa egyenlő, mivel az
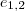
egyenes része; hasonlóan
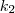
és
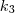
körökre vonatkozó hatványa egyenlő, mivel az
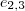
egyenes része. Következésképp a
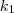
és
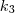
körre vonatkozó hatványa is egyenlő, tehát
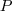
rajta van
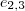
hatványvonalon, így a három hatványvonal egy pontban metszi egymást. Ebből a pontból mindhárom körre vonatkozó hatvány egyenlő. Mindegy, hogy a körök metszik, érintik egymást vagy nincsen közös pontjuk, a bizonyítás akkor is igaz.
A bizonyítás során feltettük, hogy
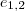
és
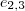
metszi egymást. Előfordulhat olyan eset, amikor ez nem igaz, tehát a két hatványvonal párhuzamos. Ekkor a körök középpontjai egy egyenesre esnek, mert
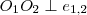
. Így a harmadik hatványvonal is párhuzamos a másik kettővel.
Olyan eset is létezik, hogy ez a három párhuzamos hatványvonal megegyezik. Ekkor ez a három kör egy
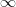
kört tartalmazó körsor tagja.
Tekinthetünk három nulla sugarú kört is. Ekkor a három "csúcs" egy háromszöget alkot, melynek hatványvonalai az oldalfelező merőlegesek. Így az oldalfelező merőlegesek is egy pontban metszik egymást.
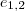 és
és 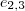 hatványvonalát! Nevezzük a metszéspontot
hatványvonalát! Nevezzük a metszéspontot 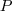 -nek. A
-nek. A 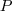 pont
pont 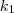 és
és 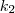 körökre vonatkozó hatványa egyenlő, mivel az
körökre vonatkozó hatványa egyenlő, mivel az 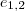 egyenes része; hasonlóan
egyenes része; hasonlóan 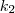 és
és 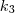 körökre vonatkozó hatványa egyenlő, mivel az
körökre vonatkozó hatványa egyenlő, mivel az 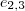 egyenes része. Következésképp a
egyenes része. Következésképp a 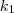 és
és 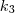 körre vonatkozó hatványa is egyenlő, tehát
körre vonatkozó hatványa is egyenlő, tehát 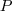 rajta van
rajta van 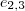 hatványvonalon, így a három hatványvonal egy pontban metszi egymást. Ebből a pontból mindhárom körre vonatkozó hatvány egyenlő. Mindegy, hogy a körök metszik, érintik egymást vagy nincsen közös pontjuk, a bizonyítás akkor is igaz.
hatványvonalon, így a három hatványvonal egy pontban metszi egymást. Ebből a pontból mindhárom körre vonatkozó hatvány egyenlő. Mindegy, hogy a körök metszik, érintik egymást vagy nincsen közös pontjuk, a bizonyítás akkor is igaz.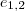 és
és 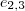 metszi egymást. Előfordulhat olyan eset, amikor ez nem igaz, tehát a két hatványvonal párhuzamos. Ekkor a körök középpontjai egy egyenesre esnek, mert
metszi egymást. Előfordulhat olyan eset, amikor ez nem igaz, tehát a két hatványvonal párhuzamos. Ekkor a körök középpontjai egy egyenesre esnek, mert 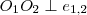 . Így a harmadik hatványvonal is párhuzamos a másik kettővel.
. Így a harmadik hatványvonal is párhuzamos a másik kettővel.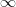 kört tartalmazó körsor tagja.
kört tartalmazó körsor tagja.




