Az oldal tölt...
184
184
| Kategória: |
Megoldás
- Feladat
|
Évfolyam: |
9. |
| Kulcsszó: |
Kör |
Lektorálás: |
Nem lektorált |
Két kör hatványvonala
Megoldás
Helyezzük a két kör koordinátarendszerbe! Az
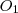
középpontú,
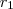
sugarú kör legyen az origóban; míg az
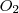
középpontú,
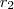
sugarú kör középpontjának koordinátája legyen
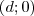
! Vegyünk fel egy
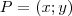
pontot, ahonnan két egyenlő
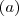
hosszúságú érintő húzható a két körhöz!
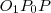
és
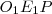
háromszögek derékszögűek, mivel a sugár merőleges a hozzá tartozó érintőre, ráadásul megegyezik az átfogójuk is. Írjuk fel a Pitagorasz-tételt mindkét háromszögre!
Hasonlóan
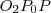
és
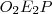
derékszögű háromszögekre:
A fölső egyenletből az alsót kivonjuk.
A levezetés során kiesett az
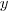
, így ettől független a megoldások mértani helye. Mivel
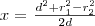
rögzített, így ezen, az

tengelyre, a két kör középpontjának egyenesére merőlegesen helyezkednek el a keresett pontok. A megoldásból látszik, hogy a két kör középpontja által meghatározott szakasz felezőpontjától
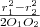
távolságra lesz a merőleges egyenes

tengellyel vett metszéspontja.
Ha a két kör metszi egymást, akkor ennek a merőleges egyenesnek lesznek olyan pontjai, ami a körökön belül van, így innen nem húzható érintő. Fogalmazzuk át a feladatot! "Adjuk meg azon pontok mértani helyét a síkon, ahonnan a pont két adott körre vonatkozó hatványa egyenlő!" Így a belső pontokra is értelmezhetjük a feladatot, tehát az egész egyenes jó megoldást ad. Ezt nevezzük hatványvonalnak.
A levezetés során leosztottunk
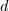
-vel, így meg kell néznünk az esetet, amikor
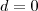
, tehát amikor a két kör középpontja egy pontba esik, tehát
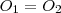
.
Teljesen hasonlóan a fenti levezetéshez, itt is egyenlővé tesszük a két egyenletet, amelyet a Pitagorasz-tétel segítségével írtunk föl.
A fölső egyenletből az alsót kivonva:
Látszik, hogy
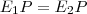
egyenlőség csak akkor áll fönn, ha

. Tehát ha a körök középpontja megegyezik, akkor csak úgy lehet egy pont e két körre vonatkozó hatványa egyenlő, ha a két körnek egyenlő a sugara is, tehát ha a két kör teljesen megegyezik. Ebben az esetben a sík bármelyik pontjából egyenlő a körökre vonatkozó hatvány.
Diszkusszió
Ha a két kör metszi egymást, akkor a hatványvonal a metszéspontokon átmenő egyenes, mivel a két metszéspont körökre vonatkozó hatványa mindkét esetben 0. Így ez a két pont rajta van a keresett egyenesen, de meg is határozza azt.
Ha a két egyenes érinti egymást (akár kívülről, akár belülről), akkor a hatványvonal az érintési ponton áthaladó,
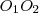
szakaszra merőleges egyenes lesz, mert az érintési pont a körökre vonatkozó hatvány 0, és merőlegesnek kell lennie
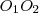
szakaszra.
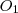 középpontú,
középpontú, 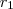 sugarú kör legyen az origóban; míg az
sugarú kör legyen az origóban; míg az 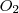 középpontú,
középpontú, 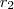 sugarú kör középpontjának koordinátája legyen
sugarú kör középpontjának koordinátája legyen 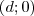 ! Vegyünk fel egy
! Vegyünk fel egy 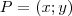 pontot, ahonnan két egyenlő
pontot, ahonnan két egyenlő 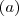 hosszúságú érintő húzható a két körhöz!
hosszúságú érintő húzható a két körhöz! 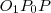 és
és 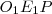 háromszögek derékszögűek, mivel a sugár merőleges a hozzá tartozó érintőre, ráadásul megegyezik az átfogójuk is. Írjuk fel a Pitagorasz-tételt mindkét háromszögre!
háromszögek derékszögűek, mivel a sugár merőleges a hozzá tartozó érintőre, ráadásul megegyezik az átfogójuk is. Írjuk fel a Pitagorasz-tételt mindkét háromszögre!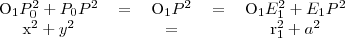
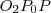 és
és 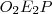 derékszögű háromszögekre:
derékszögű háromszögekre: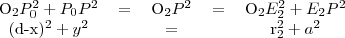
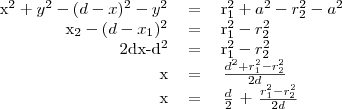
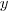 , így ettől független a megoldások mértani helye. Mivel
, így ettől független a megoldások mértani helye. Mivel 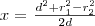 rögzített, így ezen, az
rögzített, így ezen, az  tengelyre, a két kör középpontjának egyenesére merőlegesen helyezkednek el a keresett pontok. A megoldásból látszik, hogy a két kör középpontja által meghatározott szakasz felezőpontjától
tengelyre, a két kör középpontjának egyenesére merőlegesen helyezkednek el a keresett pontok. A megoldásból látszik, hogy a két kör középpontja által meghatározott szakasz felezőpontjától 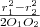 távolságra lesz a merőleges egyenes
távolságra lesz a merőleges egyenes  tengellyel vett metszéspontja.
tengellyel vett metszéspontja.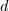 -vel, így meg kell néznünk az esetet, amikor
-vel, így meg kell néznünk az esetet, amikor 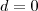 , tehát amikor a két kör középpontja egy pontba esik, tehát
, tehát amikor a két kör középpontja egy pontba esik, tehát 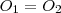 .
.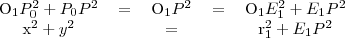
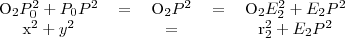
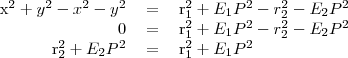
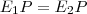 egyenlőség csak akkor áll fönn, ha
egyenlőség csak akkor áll fönn, ha  . Tehát ha a körök középpontja megegyezik, akkor csak úgy lehet egy pont e két körre vonatkozó hatványa egyenlő, ha a két körnek egyenlő a sugara is, tehát ha a két kör teljesen megegyezik. Ebben az esetben a sík bármelyik pontjából egyenlő a körökre vonatkozó hatvány.
. Tehát ha a körök középpontja megegyezik, akkor csak úgy lehet egy pont e két körre vonatkozó hatványa egyenlő, ha a két körnek egyenlő a sugara is, tehát ha a két kör teljesen megegyezik. Ebben az esetben a sík bármelyik pontjából egyenlő a körökre vonatkozó hatvány.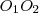 szakaszra merőleges egyenes lesz, mert az érintési pont a körökre vonatkozó hatvány 0, és merőlegesnek kell lennie
szakaszra merőleges egyenes lesz, mert az érintési pont a körökre vonatkozó hatvány 0, és merőlegesnek kell lennie 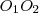 szakaszra.
szakaszra.




