Az oldal tölt...
180
180
| Kategória: |
Bizonyítás
- Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Pont körre vonatkozó hatványa |
Lektorálás: |
Nem lektorált |
A szelőtétel
Bizonyítás
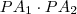
állandóságát bizonyíthatjuk úgy is fölveszünk egy másik szelőt és bebizonyítjuk a
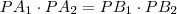
egyenletet.
Belső pontra
Mivel
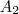
és
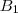
pont is az
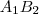
húr látókörén van rajta, így "A középponti és kerületi szögek tételé"-nek értelmében:
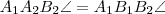
.
Hasonlóan
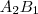
húrra:
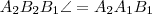
.
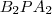
és
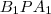
szögek csúcsszögek, így
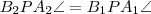
.
Tehát
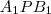
és
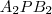
háromszögeknek minden szöge páronként egyenlő, így
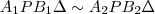
.
Így a következő aránypár fölírható:
Most húzzuk be azt a szelőt, amely tartalmazza a
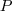
és
pontokat! Erre is igazak a fönt bizonyítottak, így
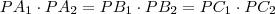
.
Az ábrából leolvasható, hogy
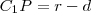
, és

, mivel előjelesen értelmezzük a szakaszokat (
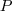
az egyenes origója és
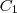
felé van a pozitív irány). Ezt behelyettesítve:
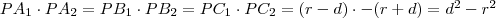
.
Külső pontra
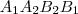
négyszög húrnégyszög, így
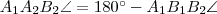
és
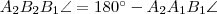
. Az ábrából kiolvasható, hogy
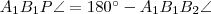
és
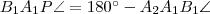
. Összegezve:
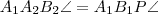
és

, amiből következik, hogy
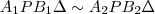
.
Így a következő aránypárt írhatjuk föl:
Most húzzuk be azt a szelőt, amely tartalmazza a
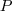
és
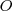
pontokat! Erre is igazak a fönt bizonyítottak, így
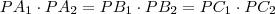
.
Az ábrából leolvasható, hogy
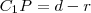
, és
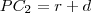
. Ezt behelyettesítve:
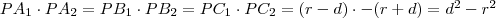
.
Vegyük azt a szélsőséges esetet, amikor a szelő érinti a kört! Ekkor a két metszéspont megegyezik, jelöljük ezt a pontot
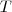
-vel! A
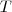
pont
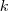
körre vonatkozó hatványa
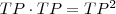
.
Írjuk fel a Pitagorasz-tételt
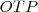
háromszögre!
I.
II.
Az
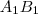
oldal közös húrja
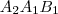
és
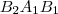
háromszögeknek, így
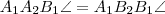
.
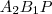
és
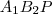
háromszögekben az
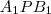
szög is megegyezik, így
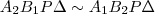
. A következő aránypár írható fel:
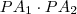 állandóságát bizonyíthatjuk úgy is fölveszünk egy másik szelőt és bebizonyítjuk a
állandóságát bizonyíthatjuk úgy is fölveszünk egy másik szelőt és bebizonyítjuk a 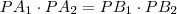 egyenletet.
egyenletet.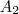 és
és 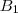 pont is az
pont is az 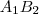 húr látókörén van rajta, így "A középponti és kerületi szögek tételé"-nek értelmében:
húr látókörén van rajta, így "A középponti és kerületi szögek tételé"-nek értelmében: 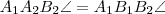 .
.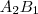 húrra:
húrra: 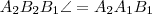 .
.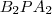 és
és 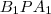 szögek csúcsszögek, így
szögek csúcsszögek, így 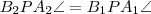 .
.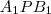 és
és 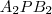 háromszögeknek minden szöge páronként egyenlő, így
háromszögeknek minden szöge páronként egyenlő, így 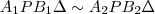 .
.
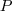 és
és 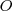 pontokat! Erre is igazak a fönt bizonyítottak, így
pontokat! Erre is igazak a fönt bizonyítottak, így 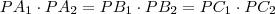 .
.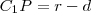 , és
, és  , mivel előjelesen értelmezzük a szakaszokat (
, mivel előjelesen értelmezzük a szakaszokat ( az egyenes origója és
az egyenes origója és  felé van a pozitív irány). Ezt behelyettesítve:
felé van a pozitív irány). Ezt behelyettesítve: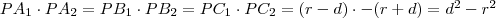 .
.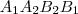 négyszög húrnégyszög, így
négyszög húrnégyszög, így 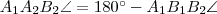 és
és 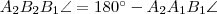 . Az ábrából kiolvasható, hogy
. Az ábrából kiolvasható, hogy 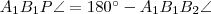 és
és 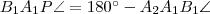 . Összegezve:
. Összegezve: 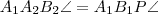 és
és  , amiből következik, hogy
, amiből következik, hogy 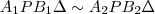 .
.
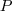 és
és 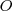 pontokat! Erre is igazak a fönt bizonyítottak, így
pontokat! Erre is igazak a fönt bizonyítottak, így 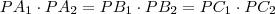 .
. 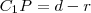 , és
, és 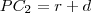 . Ezt behelyettesítve:
. Ezt behelyettesítve: 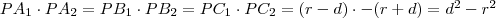 .
.  -vel! A
-vel! A  pont
pont  körre vonatkozó hatványa
körre vonatkozó hatványa 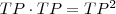 .
.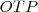 háromszögre!
háromszögre! 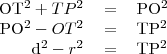
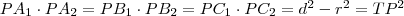
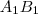 oldal közös húrja
oldal közös húrja 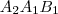 és
és 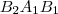 háromszögeknek, így
háromszögeknek, így 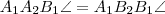 .
. 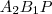 és
és 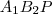 háromszögekben az
háromszögekben az 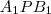 szög is megegyezik, így
szög is megegyezik, így 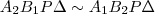 . A következő aránypár írható fel:
. A következő aránypár írható fel:





