Az oldal tölt...
175
175
| Kategória: |
Bizonyítás
- Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Terület-felszín (lásd még:05.DB) |
Lektorálás: |
Nem lektorált |
A Héron-képlet
Bizonyítás
I.
Tudjuk, hogy a

oldalhoz tartozó magasságvonal hossza:
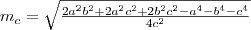
.
II.
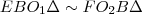
, mert az oldalak páronként merőlegesek egymásra. (A belső szögfelező merőleges a külső szögfelezőre
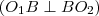
, másrészt a sugárhoz tartozó érintő merőleges a sugárra.) Így a következő aránypár írható föl:
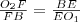
.
"A beírt kör érintőpontjainak távolsága a csúcsoktól" című bizonyításból tudjuk, hogy
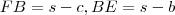
. Továbbá az ábrából kiolvasható, hogy
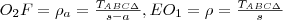
. Ezeket behelyettesítjük az aránypárba.
 oldalhoz tartozó magasságvonal hossza:
oldalhoz tartozó magasságvonal hossza: 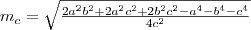 .
.![\begin{tabular}{rcl}
T_{ABC\Delta}&=&\left{\frac{c\cdot m_c}{2}\right} \\
&=&\left{\frac{c\cdot \sqrt{\frac{2a^2b^2+2a^2c^2+2b^2c^2-a^4-b^4-c^4}{4c^2}}}{2}\right} \\
&=&\sqrt{\frac{2a^2b^2+2a^2c^2+2b^2c^2-a^4-b^4-c^4}{16}} \\
&=&\sqrt{\frac{(a^2c^2+2abc^2+b^2c^2)-(a^4-2a^2b^2+b^4)-c^4+(a^2c^2-2abc^2+b^2c^2)}{16}} \\
&=&\sqrt{\frac{(a^2+2ab+b^2)c^2-(a^2-b^2)^2-c^4+(a^2-2ab+b^2)c^2}{16}} \\
&=&\sqrt{\frac{(a+b)^2c^2-\big[(a+b)(a-b)\big]^2-c^4+(a-b)^2c^2}{16}} \\
&=&\sqrt{\frac{(a+b)^2c^2-(a+b)^2(a-b)^2-c^4+(a-b)^2c^2}{16}} \\
&=&\sqrt{\frac{\big[(a+b)^2-c^2\big]\cdot\big[c^2-(a-b)^2\big]}{16}} \\
&=&\sqrt{\frac{\big[(a+b+c)(a+b-c)\big]\cdot\big[(c+a-b)(c-a+b)\big]}{16}} \\
&=&\sqrt{\frac{(a+b+c)(a+b-c)(a-b+c)(-a+b+c)}{16}} \\
&=&\sqrt{\left(\frac{a+b+c}{2}\right)\left(\frac{a+b-c}{2}\right)\left(\frac{a-b+c}{2}\right)\left(\frac{-a+b+c}{2}\right)} \\
&=&\sqrt{\left(\frac{a+b+c}{2}\right)\left(\frac{a+b+c}{2}-c\right)\left(\frac{a+b+c}{2}-b\right)\left(\frac{a+b+c}{2}-a\right)} \\
\end{tabular} \begin{tabular}{rcl}
T_{ABC\Delta}&=&\left{\frac{c\cdot m_c}{2}\right} \\
&=&\left{\frac{c\cdot \sqrt{\frac{2a^2b^2+2a^2c^2+2b^2c^2-a^4-b^4-c^4}{4c^2}}}{2}\right} \\
&=&\sqrt{\frac{2a^2b^2+2a^2c^2+2b^2c^2-a^4-b^4-c^4}{16}} \\
&=&\sqrt{\frac{(a^2c^2+2abc^2+b^2c^2)-(a^4-2a^2b^2+b^4)-c^4+(a^2c^2-2abc^2+b^2c^2)}{16}} \\
&=&\sqrt{\frac{(a^2+2ab+b^2)c^2-(a^2-b^2)^2-c^4+(a^2-2ab+b^2)c^2}{16}} \\
&=&\sqrt{\frac{(a+b)^2c^2-\big[(a+b)(a-b)\big]^2-c^4+(a-b)^2c^2}{16}} \\
&=&\sqrt{\frac{(a+b)^2c^2-(a+b)^2(a-b)^2-c^4+(a-b)^2c^2}{16}} \\
&=&\sqrt{\frac{\big[(a+b)^2-c^2\big]\cdot\big[c^2-(a-b)^2\big]}{16}} \\
&=&\sqrt{\frac{\big[(a+b+c)(a+b-c)\big]\cdot\big[(c+a-b)(c-a+b)\big]}{16}} \\
&=&\sqrt{\frac{(a+b+c)(a+b-c)(a-b+c)(-a+b+c)}{16}} \\
&=&\sqrt{\left(\frac{a+b+c}{2}\right)\left(\frac{a+b-c}{2}\right)\left(\frac{a-b+c}{2}\right)\left(\frac{-a+b+c}{2}\right)} \\
&=&\sqrt{\left(\frac{a+b+c}{2}\right)\left(\frac{a+b+c}{2}-c\right)\left(\frac{a+b+c}{2}-b\right)\left(\frac{a+b+c}{2}-a\right)} \\
\end{tabular}](libraries/modulok/latexesszoveg/media/latex/43229d0cdb5048c119ed183cf1c81b64.png)
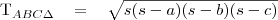
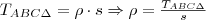
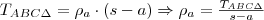
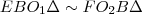 , mert az oldalak páronként merőlegesek egymásra. (A belső szögfelező merőleges a külső szögfelezőre
, mert az oldalak páronként merőlegesek egymásra. (A belső szögfelező merőleges a külső szögfelezőre 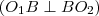 , másrészt a sugárhoz tartozó érintő merőleges a sugárra.) Így a következő aránypár írható föl:
, másrészt a sugárhoz tartozó érintő merőleges a sugárra.) Így a következő aránypár írható föl: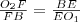 .
.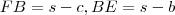 . Továbbá az ábrából kiolvasható, hogy
. Továbbá az ábrából kiolvasható, hogy 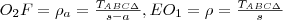 . Ezeket behelyettesítjük az aránypárba.
. Ezeket behelyettesítjük az aránypárba.