Keresés
Legújabb cikkek
- Daniell-elem - definíció
- Akkumulátor - definíció
- Szárazelem - definíció
- Galvánelem - definíció
- Kirchhoff II. törvénye (huroktörvény) - törvény
Támogató
Szabványok
| Kategória: | Megoldás - Feladat | Évfolyam: | 9. |
| Kulcsszó: | Belső szögek felezői | Lektorálás: | Nem lektorált |
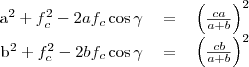
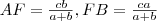, mert 
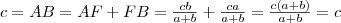és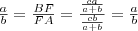 
.
-szereséből vonjuk ki az alsó 
-szorosát!![\begin{tabular}{rcl}
ba^2+bf_c^2-2abf_c\cos\gamma-ab^2-af_c^2+2abf_c\cos\gamma&=&\left{\frac{a^2bc^2-ab^2c^2}{(a+b)^2}\right} \\
ba^2+bf_c^2-ab^2-af_c^2&=&\left{\frac{a^2bc^2-ab^2c^2}{(a+b)^2}\right} \\
ab(a-b)-f_c^2(a-b)&=&\left{\frac{abc^2(a-b)}{(a+b)^2} \\
ab-f_c^2&=&\left{\frac{abc^2}{(a+b)^2} \\
f_c^2&=&\left{\frac{(a+b)^2ab-abc^2}{(a+b)^2} \\
f_c&=&\left{\frac{\sqrt{ab\big[(a+b)^2-c^2\big]}}{a+b} \\
\end{tabular}](libraries/modulok/latexesszoveg/media/latex/e19bd9c07823ada11ba04a6de0156a37.png "\begin{tabular}{rcl}
ba^2+bf_c^2-2abf_c\cos\gamma-ab^2-af_c^2+2abf_c\cos\gamma&=&\left{\frac{a^2bc^2-ab^2c^2}{(a+b)^2}\right} \\
ba^2+bf_c^2-ab^2-af_c^2&=&\left{\frac{a^2bc^2-ab^2c^2}{(a+b)^2}\right} \\
ab(a-b)-f_c^2(a-b)&=&\left{\frac{abc^2(a-b)}{(a+b)^2} \\
ab-f_c^2&=&\left{\frac{abc^2}{(a+b)^2} \\
f_c^2&=&\left{\frac{(a+b)^2ab-abc^2}{(a+b)^2} \\
f_c&=&\left{\frac{\sqrt{ab\big[(a+b)^2-c^2\big]}}{a+b} \\
\end{tabular}")
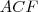és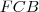 
háromszögekre!
