Az oldal tölt...
162
162
| Kategória: |
Bizonyítás
- Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Trigonometrikus azonosságok (lásd még:04.BD és 04.CD) |
Lektorálás: |
Nem lektorált |
Az addíciós (összegzési) képletek
Bizonyítás
Így
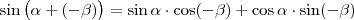
is igaz. Bizonyított, hogy
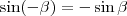
és
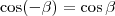
. Ezt beírva a fönti egyenletbe:
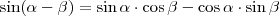
.
Mivel
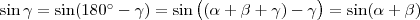
, ezért
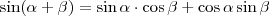
.
Összegezve:
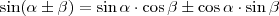
Így
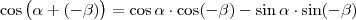
is igaz. Bizonyított, hogy
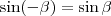
és
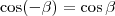
. Ezt beírva a fönti egyenletbe:
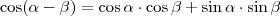
.
Összegezve:
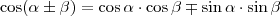
Vegyünk egy olyan

,
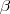
és
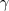
szögű háromszöget, amely köréírt körének sugara egységnyi! Húzzuk be mindhárom magasságvonalat! A kapott szakaszok közül néhányat a következőkben kifejezzük a szögek segítségével.
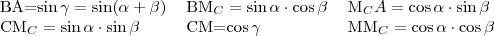
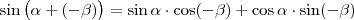 is igaz. Bizonyított, hogy
is igaz. Bizonyított, hogy 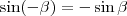 és
és 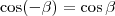 . Ezt beírva a fönti egyenletbe:
. Ezt beírva a fönti egyenletbe: 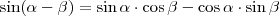 .
.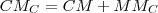
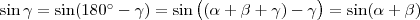 , ezért
, ezért 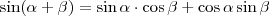 .
.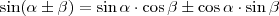
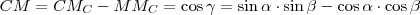
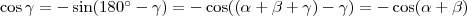 , ezért
, ezért 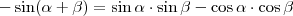 , így
, így 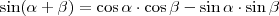
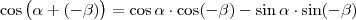 is igaz. Bizonyított, hogy
is igaz. Bizonyított, hogy 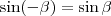 és
és 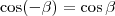 . Ezt beírva a fönti egyenletbe:
. Ezt beírva a fönti egyenletbe: 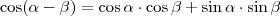 .
.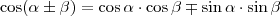
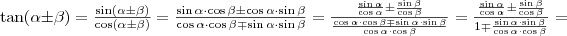
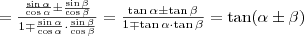
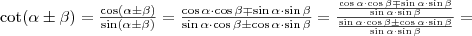
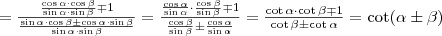
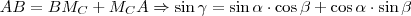
 ,
, 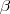 és
és 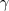 szögű háromszöget, amely köréírt körének sugara egységnyi! Húzzuk be mindhárom magasságvonalat! A kapott szakaszok közül néhányat a következőkben kifejezzük a szögek segítségével.
szögű háromszöget, amely köréírt körének sugara egységnyi! Húzzuk be mindhárom magasságvonalat! A kapott szakaszok közül néhányat a következőkben kifejezzük a szögek segítségével.




