Keresés

Legújabb cikkek

Daniell-elem - definíció
Akkumulátor - definíció
Szárazelem - definíció
Galvánelem - definíció
Kirchhoff II. törvénye (huroktörvény) - törvény

Támogató

Szabványok

153 153

Kategória:	Megoldás - Feladat	Évfolyam:	9.
Kulcsszó:	Magasságok	Lektorálás:	Nem lektorált

A magasságvonal hossza

Megoldás

$x^2+m_c^2=a^2$

$(c-x)^2+m_c^2=b^2$

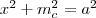
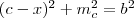
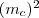Ezekből kifejezzük $(m_c)^2$ -t, és ezeket egyenlővé tesszük: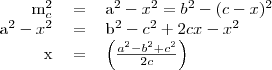

$\begin{tabular}{rcl} m_c^2 & = & a^2-x^2=b^2-(c-x)^2 \\ a^2-x^2 & = & b^2-c^2+2cx-x^2 \\ x & = & \left(\frac{a^2-b^2+c^2}{2c}\right) \end{tabular}$

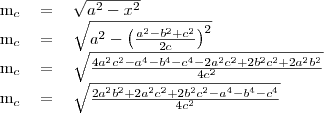
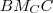Ezt visszahelyettesítve:

$\begin{tabular}{rcl} &&\\ m_c&=&\sqrt{a^2-x^2} \\ m_c&=&\sqrt{a^2-\left(\frac{a^2-b^2+c^2}{2c}\right)^2} \\ m_c&=&\sqrt{\frac{4a^2c^2-a^4-b^4-c^4-2a^2c^2+2b^2c^2+2a^2b^2}{4c^2}} \\ m_c&=&\sqrt{\frac{2a^2b^2+2a^2c^2+2b^2c^2-a^4-b^4-c^4}{4c^2}}\end{tabular}$

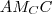Írjuk föl a Pitagorasz-tételt a $BM_CC$ és $AM_CC$ háromszögekre!

Kezdés

Cikkek