Az oldal tölt...
151
151
| Kategória: |
Megoldás
- Feladat
|
Évfolyam: |
9. |
| Kulcsszó: |
Súlyvonalak |
Lektorálás: |
Nem lektorált |
A súlyvonal hossza
Tükrözzük a háromszöget
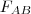
-re! A középpontos tükrözés tulajdonságai miatt
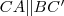
és
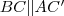
, tehát egy paralelogrammát kaptunk. Erre felírhatjuk "A paralelogrammatételt", majd ezt rendezzük
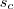
-re!
Ha
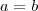
, akkor egy egyenlőszárú háromszög magasságát kell kiszámolnunk. Írjuk föl a Pitagorasz-tételt a magasságvonal (súlyvonal), az egyik szár és az alap fele által meghatározott derékszögű háromszögre!
I.
II.
A
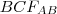
, majd a
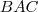
háromszögre írjuk föl a koszinusztételt!
Most vonjuk ki a felső egyenletből az alsó egyenlet felét!
III.
Írjuk föl a koszinusztételt a
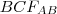
, majd az
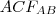
háromszögre!
Ismeretes, hogy
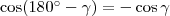
Így a két egyenletet összeadva:
IV.
Tudjuk, hogy a súlyvonal felezi a háromszög területét. Így a két kisháromszögre
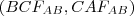
felírva a Hérón-képletet, ezek egyenlők lesznek. Ez az egyenlet csak a súlyvonal hosszát tartalmazza ismeretlenként, így ebből ez kifejezhető.
Az
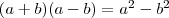
összefüggést használva az első-második és a harmadik-negyedik tagra:
Közös nevezőre hozunk az egyes zárójeleken belül:
Kibontjuk a zárójeleket:
Nullára rendezzük az egyenletet, és kiemelünk

-t:
Leosztunk

-tel: (
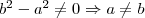
)
$\begin{tabular}{rcl}
a^2=s_c^2+\left(\frac{c}{2}\right)^2 \Rightarrow s_c^2
Megoldás
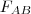 -re! A középpontos tükrözés tulajdonságai miatt
-re! A középpontos tükrözés tulajdonságai miatt 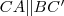 és
és 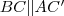 , tehát egy paralelogrammát kaptunk. Erre felírhatjuk "A paralelogrammatételt", majd ezt rendezzük
, tehát egy paralelogrammát kaptunk. Erre felírhatjuk "A paralelogrammatételt", majd ezt rendezzük 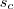 -re!
-re!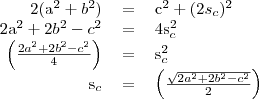
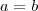 , akkor egy egyenlőszárú háromszög magasságát kell kiszámolnunk. Írjuk föl a Pitagorasz-tételt a magasságvonal (súlyvonal), az egyik szár és az alap fele által meghatározott derékszögű háromszögre!
, akkor egy egyenlőszárú háromszög magasságát kell kiszámolnunk. Írjuk föl a Pitagorasz-tételt a magasságvonal (súlyvonal), az egyik szár és az alap fele által meghatározott derékszögű háromszögre!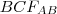 , majd a
, majd a 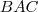 háromszögre írjuk föl a koszinusztételt!
háromszögre írjuk föl a koszinusztételt!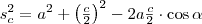
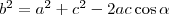
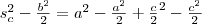
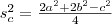
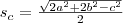
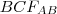 , majd az
, majd az 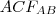 háromszögre!
háromszögre!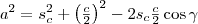
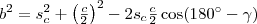
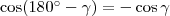
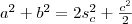
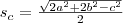
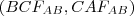 felírva a Hérón-képletet, ezek egyenlők lesznek. Ez az egyenlet csak a súlyvonal hosszát tartalmazza ismeretlenként, így ebből ez kifejezhető.
felírva a Hérón-képletet, ezek egyenlők lesznek. Ez az egyenlet csak a súlyvonal hosszát tartalmazza ismeretlenként, így ebből ez kifejezhető. 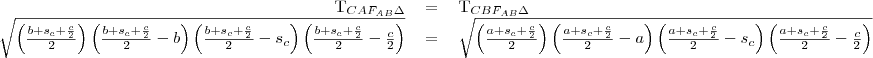
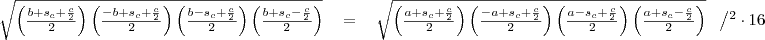
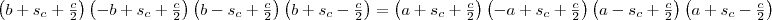
![\left[\left(s_c+\frac{c}{2}\right)^2-b^2\right]\left[b^2-\left(\frac{c}{2}-s_c\right)^2\right]=\left[\left(s_c+\frac{c}{2}\right)^2-a^2\right]\left[a^2-\left(\frac{c}{2}-s_c\right)^2\right] \left[\left(s_c+\frac{c}{2}\right)^2-b^2\right]\left[b^2-\left(\frac{c}{2}-s_c\right)^2\right]=\left[\left(s_c+\frac{c}{2}\right)^2-a^2\right]\left[a^2-\left(\frac{c}{2}-s_c\right)^2\right]](libraries/modulok/latexesszoveg/media/latex/da03b89b5060846968db74b314a2454c.png)
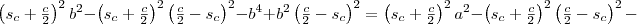
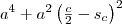
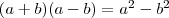 összefüggést használva az első-második és a harmadik-negyedik tagra:
összefüggést használva az első-második és a harmadik-negyedik tagra: -t:
-t: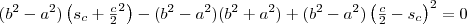
 -tel: (
-tel: (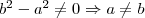 )
)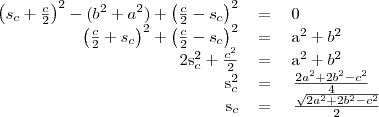
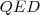
![\left[\left(s_c+\frac{c}{2}\right)+b\right]\left[\left(s_c+\frac{c}{2}\right)-b\right]-\left[b+\left(\frac{c}{2}-s_c\right)\right]\left[b-\left(\frac{c}{2}-s_c\right)\right]=\left[\left(s_c+\frac{c}{2}\right)+a\right]\left[\left(s_c+\frac{c}{2}\right)-a\right]-\left[a+\left(\frac{c}{2}-s_c\right)\right]\left[a-\left(\frac{c}{2}-s_c\right)\right] \left[\left(s_c+\frac{c}{2}\right)+b\right]\left[\left(s_c+\frac{c}{2}\right)-b\right]-\left[b+\left(\frac{c}{2}-s_c\right)\right]\left[b-\left(\frac{c}{2}-s_c\right)\right]=\left[\left(s_c+\frac{c}{2}\right)+a\right]\left[\left(s_c+\frac{c}{2}\right)-a\right]-\left[a+\left(\frac{c}{2}-s_c\right)\right]\left[a-\left(\frac{c}{2}-s_c\right)\right]](libraries/modulok/latexesszoveg/media/latex/802154893f14e508b29befc81cbbac81.png)





