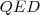Az oldal tölt...
131
131
| Kategória: |
Bizonyítás
- Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Belső szögek felezői |
Lektorálás: |
Nem lektorált |
A belsőszögfelező-tétel
Bizonyítás
I.
Hosszabbítsuk meg az

oldalt

-vel, legyen ez a pont
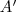
. Ekkor
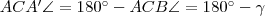
! Az
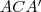
háromszög egyenlőszárú
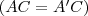
, tehát
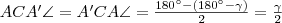
. Mivel
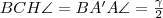
, így
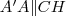
.
Erre fölírva a párhuzamos szelők tételét:
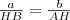
, rendezve:
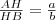
.
II.a
Írjuk föl a szinusztételt
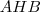
, majd
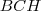
háromszögekre!
II.b
Hasonlóan írjuk föl a szinusztételt
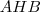
, majd
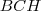
háromszögekre!
Ismeretes, hogy
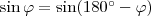
.
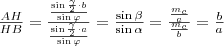
III.
Mivel a szögfelező minden pontja egyenlő távol van a szög két szárától, így
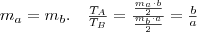
Tehát
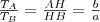
.
IV.
Mivel
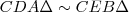
, így
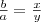
.
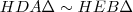
, ezért
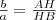
.
 oldalt
oldalt  -vel, legyen ez a pont
-vel, legyen ez a pont 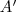 . Ekkor
. Ekkor 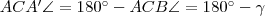 ! Az
! Az 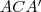 háromszög egyenlőszárú
háromszög egyenlőszárú 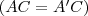 , tehát
, tehát 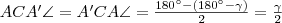 . Mivel
. Mivel 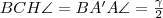 , így
, így 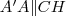 .
.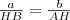 , rendezve:
, rendezve: 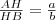 .
.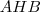 , majd
, majd 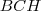 háromszögekre!
háromszögekre!
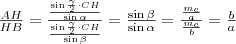
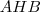 , majd
, majd 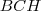 háromszögekre!
háromszögekre! 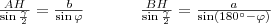
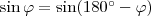 .
. 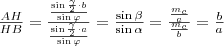
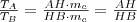
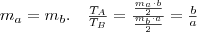
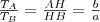 .
.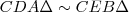 , így
, így 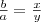 .
.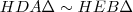 , ezért
, ezért 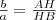 .
.