Az oldal tölt...
127
127
| Kategória: |
Bizonyítás
- Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Kerületi-középponti szögek |
Lektorálás: |
Nem lektorált |
A kerületi és középponti szögek tételének megfordítása
Bizonyítás
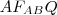
és
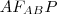
háromszögben
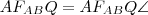
. Mivel
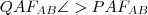
(a háromszög belső szögeinek állandósága miatt)
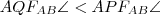
. Hasonlóan a
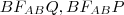
háromszögekben
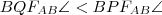
.
A föntebb fölírt két egyenlőtlenséget összeadjuk:
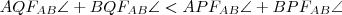
. Az ábrából észrevehető, hogy a bal oldalon pont
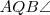
, míg a jobb oldalon
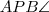
található.
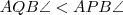
, tehát nem
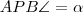
-ben látszik
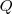
-ból az
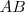
húr.
I.
Teljesen hasonlóan beláthatjuk, hogy belső pontból se ugyanabban a szögből látszik. Ekkor azonban a következő egyenlőtlenségek írhatóak föl:
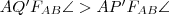
és
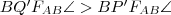
, amik a
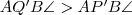
egyenlőtlenségre vezetnek.
II.
A
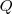
(vagy
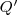
) pontos keresztül húzzuk meg a látókört. A föntiekhez hasonló módon belátjuk, hogy a középponti szögek eltérnek a
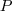
-hez (és
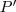
-höz) tartozó középponti szögektől, tehát a kerületi szögük sem lehet egyenlő.
Vegyünk fel egy
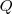
pontot az

körön kívül. Kössük ez össze
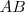
szakasz felezőpontjával,
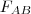
-vel. Ennek a metszéspontja az

körrel legyen
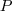
!
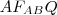 és
és 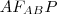 háromszögben
háromszögben 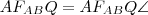 . Mivel
. Mivel 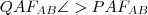 (a háromszög belső szögeinek állandósága miatt)
(a háromszög belső szögeinek állandósága miatt) 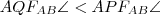 . Hasonlóan a
. Hasonlóan a 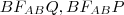 háromszögekben
háromszögekben 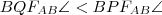 .
.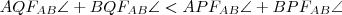 . Az ábrából észrevehető, hogy a bal oldalon pont
. Az ábrából észrevehető, hogy a bal oldalon pont 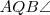 , míg a jobb oldalon
, míg a jobb oldalon 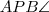 található.
található. 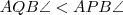 , tehát nem
, tehát nem 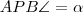 -ben látszik
-ben látszik 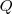 -ból az
-ból az 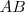 húr.
húr.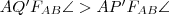 és
és 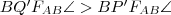 , amik a
, amik a 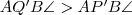 egyenlőtlenségre vezetnek.
egyenlőtlenségre vezetnek.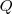 (vagy
(vagy 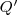 ) pontos keresztül húzzuk meg a látókört. A föntiekhez hasonló módon belátjuk, hogy a középponti szögek eltérnek a
) pontos keresztül húzzuk meg a látókört. A föntiekhez hasonló módon belátjuk, hogy a középponti szögek eltérnek a 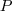 -hez (és
-hez (és 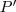 -höz) tartozó középponti szögektől, tehát a kerületi szögük sem lehet egyenlő.
-höz) tartozó középponti szögektől, tehát a kerületi szögük sem lehet egyenlő.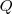 pontot az
pontot az  körön kívül. Kössük ez össze
körön kívül. Kössük ez össze 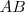 szakasz felezőpontjával,
szakasz felezőpontjával, 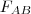 -vel. Ennek a metszéspontja az
-vel. Ennek a metszéspontja az  körrel legyen
körrel legyen 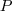 !
!




