Az oldal tölt...
125
125
| Kategória: |
Bizonyítás
- Tétel
|
Évfolyam: |
9. |
| Kulcsszó: |
Látókörív |
Lektorálás: |
Nem lektorált |
A kerületi és középponti szögek tétele
Bizonyítás
Mivel az
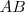
húr rögzített, így
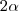
is rögzített, vagyis
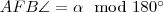
is rögzített a
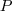
pont helyzetétől függetlenül. (Természetesen a
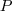
pont az

kör
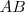
húrra vett tükrörképén is elhelyezkedhet.) Az így kapott köröket
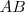
húr és

szög látóköreinek nevezzük.
Tükrözzük
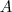
-t
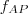
-re, így
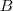
-be jutunk. Ezt tükrözzük
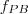
-re, így
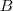
-be jutunk. Ezt
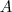
-nak egy
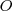
körüli,

mértékű elforgatásának foghatjuk fel "A két tengelyes tükrözés és egy elforgatás egyenértékűsége" című bizonyítás miatt. Ugyancsak ebből a bizonyításból következik, hogy a két tengely által bezárt szög
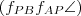
fele az elfordítás szögének, vagyis
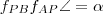
. De mivel
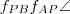
és
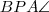
merőleges szárú szögek
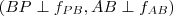
, így
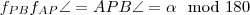
. (A jobb oldali ábrán
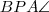
ugyan
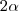
nagyságú, de ellentétes irányú, tehát
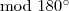
egyenlő a bal oldali ábrán szereplő
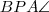
-gel.)
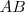 húr rögzített, így
húr rögzített, így 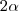 is rögzített, vagyis
is rögzített, vagyis 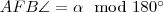 is rögzített a
is rögzített a 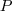 pont helyzetétől függetlenül. (Természetesen a
pont helyzetétől függetlenül. (Természetesen a 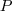 pont az
pont az  kör
kör 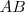 húrra vett tükrörképén is elhelyezkedhet.) Az így kapott köröket
húrra vett tükrörképén is elhelyezkedhet.) Az így kapott köröket 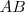 húr és
húr és  szög látóköreinek nevezzük.
szög látóköreinek nevezzük.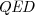
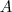 -t
-t 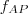 -re, így
-re, így 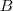 -be jutunk. Ezt tükrözzük
-be jutunk. Ezt tükrözzük 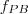 -re, így
-re, így 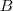 -be jutunk. Ezt
-be jutunk. Ezt 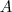 -nak egy
-nak egy 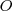 körüli,
körüli,  mértékű elforgatásának foghatjuk fel "A két tengelyes tükrözés és egy elforgatás egyenértékűsége" című bizonyítás miatt. Ugyancsak ebből a bizonyításból következik, hogy a két tengely által bezárt szög
mértékű elforgatásának foghatjuk fel "A két tengelyes tükrözés és egy elforgatás egyenértékűsége" című bizonyítás miatt. Ugyancsak ebből a bizonyításból következik, hogy a két tengely által bezárt szög 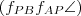 fele az elfordítás szögének, vagyis
fele az elfordítás szögének, vagyis 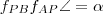 . De mivel
. De mivel 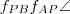 és
és 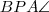 merőleges szárú szögek
merőleges szárú szögek 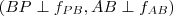 , így
, így 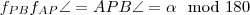 . (A jobb oldali ábrán
. (A jobb oldali ábrán 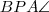 ugyan
ugyan 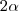 nagyságú, de ellentétes irányú, tehát
nagyságú, de ellentétes irányú, tehát 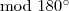 egyenlő a bal oldali ábrán szereplő
egyenlő a bal oldali ábrán szereplő 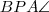 -gel.)
-gel.)




