Keresés
Legújabb cikkek
- Daniell-elem - definíció
- Akkumulátor - definíció
- Szárazelem - definíció
- Galvánelem - definíció
- Kirchhoff II. törvénye (huroktörvény) - törvény
Támogató
Szabványok
| Kategória: | Bizonyítás - Tétel | Évfolyam: | 9. |
| Kulcsszó: | Polinomok szorzattá alakítása | Lektorálás: | Nem lektorált |
(
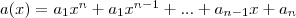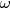az egyenlet egyik gyöke.)![\mathbb{C}[x]~~~~\omega \in \mathbb{C}](libraries/modulok/latexesszoveg/media/latex/0147e6d8c145bbd3caf02d4fea34add7.png "\mathbb{C}[x]~~~~\omega \in \mathbb{C}")
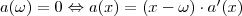
helyére 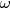-t! Ekkor ![\left[a(\omega)=0\right]=\left[(\omega-\omega)a'(x)=0\right]](libraries/modulok/latexesszoveg/media/latex/c83be527688d79857fdbfff0da62359e.png "\left[a(\omega)=0\right]=\left[(\omega-\omega)a'(x)=0\right]")
, tehát az 
irányban igaz. Innen két módon is beláthatjuk, hogy az 
irányban is igaz.![a(x)=a(x)-a(\omega)=a_0x^n-a_0\omega^n+a_1x^{n-1}-a_1\omega^{n-1}+...+a_{n-1}x-a_{n-1}\omega+a_n-a_n=\\
=a_0(x-\omega)[x^{n-1}+x^{n-2}\omega+x^{n-3}\omega^2+...+x\omega^{n-2}+\omega^{n-1}]+a_1(x-\omega)[x^{n-2}+...+\omega^{n-2}]+...+a_{n-1}(x-\omega)=\\
=(x-\omega)[x^{n-1}+x^{n-2}\omega+x^{n-3}\omega^2+...+x\omega^{n-2}+\omega^{n-1}+x^{n-2}+...+\omega^{n-2}+...+x+\omega]=(x-\omega)\cdot a'(x)](libraries/modulok/latexesszoveg/media/latex/0ed4cce520ac6f412b912cfd43e7a529.png "a(x)=a(x)-a(\omega)=a_0x^n-a_0\omega^n+a_1x^{n-1}-a_1\omega^{n-1}+...+a_{n-1}x-a_{n-1}\omega+a_n-a_n=\\
=a_0(x-\omega)[x^{n-1}+x^{n-2}\omega+x^{n-3}\omega^2+...+x\omega^{n-2}+\omega^{n-1}]+a_1(x-\omega)[x^{n-2}+...+\omega^{n-2}]+...+a_{n-1}(x-\omega)=\\
=(x-\omega)[x^{n-1}+x^{n-2}\omega+x^{n-3}\omega^2+...+x\omega^{n-2}+\omega^{n-1}+x^{n-2}+...+\omega^{n-2}+...+x+\omega]=(x-\omega)\cdot a'(x)")
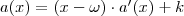
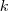a maradék a fönti osztásban. Helyettesítsünk be 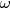-t!
. Mivel nincsen maradék, így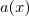 
osztható 
-val, tehát a gyök kiemelhető.
