Az oldal tölt...
100
100
| Kategória: |
Bizonyítás
|
Évfolyam: |
9. |
| Kulcsszó: |
Másodfokú (és arra visszavezethető) egyenlőtlenségek |
Lektorálás: |
Nem lektorált |
A másodfokú egyenlőtlenség általános megoldása
Levezetés
Meghatározzuk a zérushelyeket a másodfokú egyenlet megoldóképletével,
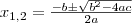
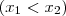
.
Ha
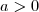
, akkor
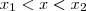
a megoldás, hiszen ha ábrázolnánk grafikonban, akkor ez a tartomány esik az x tengely alá.
Ha
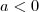
, akkor
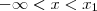
és
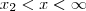
a megoldás.
Ha a diszkirimináns negatív, vagyis nincsen egy gyök se, akkor:
Ha
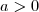
, akkor
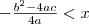
a megoldás, hiszen ekkor a parabola összes pontja nagyobb
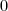
-nál.
Ha pedig
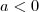
, akkor
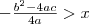
a megoldás.
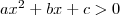
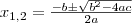
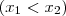 .
.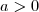 , akkor
, akkor 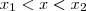 a megoldás, hiszen ha ábrázolnánk grafikonban, akkor ez a tartomány esik az x tengely alá.
a megoldás, hiszen ha ábrázolnánk grafikonban, akkor ez a tartomány esik az x tengely alá. 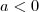 , akkor
, akkor 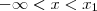 és
és 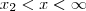 a megoldás.
a megoldás. 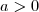 , akkor
, akkor 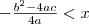 a megoldás, hiszen ekkor a parabola összes pontja nagyobb
a megoldás, hiszen ekkor a parabola összes pontja nagyobb 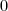 -nál.
-nál.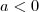 , akkor
, akkor 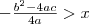 a megoldás.
a megoldás.




